题目列表(包括答案和解析)
如图所示，竖直平面内有范围足够大、水平向左的匀强电场，在虚线左侧有垂直纸面向里水平的匀强磁场，磁场的磁感强度大小为B．一粗细均匀的绝缘轨道由两段水平且足够长的直杆PQ、MN和一半径为R的半圆环MAP组成，固定在竖直平面内，半圆环与两直杆的切点P、M恰好在磁场边界线上，轨道的NMAP段光滑，PQ段粗糙，现有一质量为m、带电荷量为+q的绝缘塑料小环套在杆MN上（环的内直径比杆的直径稍大），将小环从M点右侧距离x0=4R的D点由静止释放，小环刚好能到达P点．试求：
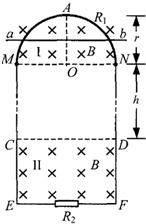如图所示，竖直平面内有一半径为r、内阻为R1、粗细均匀的光滑半圆形金属环，在M、N处与相距为2r、电阻不计的平行光滑金属轨道ME、NF相接，EF之间接有电阻R2，已知R1=12R，R2=4R．在MN上方及CD下方有水平方向的匀强磁场I和II，磁感应强度大小均为B．现有质量为m、电阻不计的导体棒ab，从半圆环的最高点A处由静止下落，在下落过程中导体棒始终保持水平，与半圆形金属环及轨道接触良好，两平行轨道中够长．已知导体棒ab下落r/2时的速度大小为v1，下落到MN处的速度大小为v2．
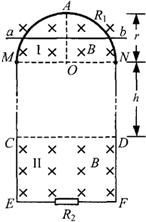如图所示，竖直平面内有一半径为r、内阻为R1、粗细均匀的光滑半圆形金属环球，在M、N处与相距为2r、电阻不计的平行光滑金属轨道ME、NF相接，EF之间接有电阻R2，已知R1=12R，R2=4R．在MN上方及CD下方有水平方向的匀强磁场I和II，磁感应强度大小均为B．现有质量为m、电阻不计的导体棒ab，从半圆环的最高点A处由静止下落，在下落过程中导体棒始终保持水平，与半圆形金属环及轨道接触良好，且平行轨道足够长．已知导体棒ab下落r/2时的速度大小为v1，下落到MN处的速度大小为v2．| r | 2 |
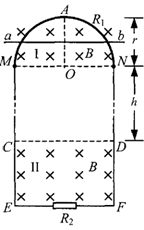（18分）如图所示，竖直平面内有一半径为r、内阻为R1、粗细均匀的光滑半圆形金属半圆环，在M、N处与相距为2r、电阻不计的平行光滑金属轨道ME、NF相接，EF之间接有电阻R2，已知R1＝12R，R2＝4R。在MN上方及CD下方有水平方向的匀强磁场I和II，磁感应强度大小均为B。现有质量为m、电阻不计的导体棒ab，从半圆环的最高点A处由静止下落，在下落过程中导体棒始终保持水平，与半圆形金属环及轨道接触良好，平行轨道足够长。已知导体棒ab下落r/2时的速度大小为v1，下落到MN处的速度大小为v2。
（1）导体棒ab从A下落r/2时的加速度大小。
（2）导体棒ab进入磁场II后棒中电流大小始终不变，求磁场I和II之间的距离h和R2上的电功率P2。
（3）若将磁场II的CD边界略微下移，导体棒ab刚进入磁场II时速度大小为v3，要使其在外力F作用下做匀加速直线运动，加速度大小为a，求所加外力F随时间变化的关系式。
如图所示，竖直平面内有一半径为r、内阻为R1、粗细均匀的光滑半圆形金属球，在M、N处与相距为2r、电阻不计的平行光滑金属轨道ME、NF相接，EF之间接有电阻R2，已知R1＝12R，R2＝4R。在MN上方及CD下方有水平方向的匀强磁场I和II，磁感应强度大小均为B。现有质量为m、电阻不计的导体棒ab，从半圆环的最高点A处由静止下落，在下落过程中导体棒始终保持水平，与半圆形金属环及轨道接触良好，高平行轨道中够长。已知导体棒ab下落r/2时的速度大小为v1，下落到MN处的速度大小为v2。
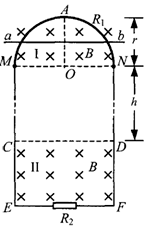（1）求导体棒ab从A下落r/2时的加速度大小。
（2）若导体棒ab进入磁场II后棒中电流大小始终不变，求磁场I和II之间的距离h和R2上的电功率P2。
（3）若将磁场II的CD边界略微下移，导体棒ab刚进入磁场II时速度大小为v3，要使其在外力F作用下做匀加速直线运动，加速度大小为a，求所加外力F随时间变化的关系式。
二、选择题(每小题6分，共48分，全对6分，对而不全3分)
题号
14
15
16
17
18
19
20
21
答案
A
B
AC
BD
AD
A
C
D
22．（1）(1)6.0（2分，6也给分）；如图(4分，电流表外接2分，滑线变组器限流接法2分) 。
(2) ①
(3分)
③ BCE (3分，BE得3分)
④纸带与打点计时器间的摩擦阻力，空气阻力等。(2分)
23．解：设子弹射入木前的速度为v，射入木块后的共同速度为V，子弹打入木块过程由动量守恒定律得：
(6分)
木块与子弹一起运动的过程由动能定理得：
(6分)
联立以上两式并代入数据得：
(4分)
24．解：（1）由于带电微粒在磁场方向反向前后的运动是对称的，所以微粒所受的电场力与重力是平衡的(2分)。微粒做匀速圆周运动，轨迹如图：
设微粒做匀速圆周运动的轨道半径为R，由图可知
①（2分）
由洛仑兹力公式及匀速圆周运动规律得：
②（2分）
联立①②解得：
③（2分）
（2）设M、N两板间的电势差为U，由电场力与重力平衡得：
④（2分）
由电容公式得：
⑤（1分）
联立④⑤得：
⑥（2分）
（3）当撤去磁场，两金属板电量减半，带电微粒做类平抛运动，竖直方向的加速度为a，由牛顿第二定律得：
⑦（2分）
带电微粒水平方向的运动：
⑧（1分）
带电微粒竖直方向的运动：
⑨（1分）
联立④⑦⑧⑨得：
⑩（2分）
25．解：（1）棒ab从A处下落
时，回路中的感生电动势为：
⑴（1分）
回路中的总电阻：
⑵（1分）
通过棒ab的电流为
⑶（1分）
由牛顿第二定律得：
⑷（2分）
联立⑴⑵⑶⑷解得：
⑸ （1分）
（2）设棒ab进入CD的速度为v3。回路中的感生电动势为：
⑹（1分）
回路中的总电阻：
⑺（1分）
通过棒ab的电流为
⑻（1分）
由平衡条件得：
⑼（1分）
棒ab从MN处下落到CD过程中，由机械能守恒定律得：
⑽（2分）
联立⑹⑺⑻⑼⑽解得：
⑾（2分）
（3）分析题意得棒ab从MN处下落h的速度与导体棒ab在磁场II中做匀速运动的速度相等（1分），设导体棒ab自进入磁场II到开始做匀速运动过程中电流产生的热量全部热量为Q总，导体棒ab移动的距离为H，则由能量守恒得：
⑿（2分）
设导体棒ab在磁场II中运动过程中的某一时刻通过R2的电流为I，则同一时刻通过R1的电流也为I，通过R3的电流为2I，电路的总功率为
⒀（1分）
所以，棒ab自进入磁场II到开始做匀速运动过程中电流产生的热量全部热量为
⒁（1分）
联立⑾⑿⒀解得：
⒂（1分）
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com