对于不等式<n＋1(n∈N^*)，某同学用数学归纳法的证明过程如下：

(1)当n＝1时，<1＋1，不等式成立．

(2)假设当n＝k(k∈N^*且k≥1)时，不等式成立，即<k＋1，则当n＝k＋1时，＝<＝＝(k＋1)＋1，

所以当n＝k＋1时，不等式成立，则上述证法                    (　　)．

A．过程全部正确

B．n＝1验得不正确

C．归纳假设不正确

D．从n＝k到n＝k＋1的推理不正确

“因为指数函数y＝a^x是增函数(大前提)，而y＝^x是指数函数(小前提)，所以函数y＝^x是增函数(结论)”，上面推理的错误在于(　　)．

A．大前提错误导致结论错

B．小前提错误导致结论错

C．推理形式错误导致结论错

D．大前提和小前提错误导致结论错

如图，正方体ABCD－A1B1C1D1的棱长为1，线段B1D1上有两个动点E、F，且EF＝，则下列结论中错误的是    (　　)

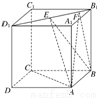
A．AC⊥BE                     B．EF∥平面ABCD

C．三棱锥A－BEF的体积为定值  D．△AEF的面积与△BEF的面积相等

 

如图所示，圆柱的高为2，底面半径为,AE、DF是圆柱的两条母线，过作圆柱的截面交下底面于.

（1）求证：；

（2）若四边形ABCD是正方形，求证；

（3）在（2）的条件下，求二面角A-BC-E的平面角的一个三角函数值。

【解析】第一问中，利用由圆柱的性质知：AD平行平面ＢＣＦＥ

又过作圆柱的截面交下底面于.∥ 

又AE、DF是圆柱的两条母线

∥ＤＦ，且ＡＥ＝ＤＦ　　　　　ＡＤ∥ＥＦ

第二问中，由线面垂直得到线线垂直。四边形ABCD是正方形　　又

BC、AE是平面ABE内两条相交直线

 

第三问中，设正方形ABCD的边长为x,则在

在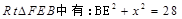 

由（2）可知：为二面角A-BC-E的平面角，所以

证明：（1）由圆柱的性质知：AD平行平面ＢＣＦＥ

又过作圆柱的截面交下底面于.∥ 

又AE、DF是圆柱的两条母线

∥ＤＦ，且ＡＥ＝ＤＦ　　　　　ＡＤ∥ＥＦ 

(2) 四边形ABCD是正方形　　又

BC、AE是平面ABE内两条相交直线

 

(3)设正方形ABCD的边长为x,则在

在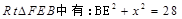 

由（2）可知：为二面角A-BC-E的平面角，所以

 

已知函数f(x)＝ax³＋bx²＋cx在x＝±1处取得极值，且在x＝0处的切线的斜率为－3.

(1)求f(x)的解析式；

(2)若过点A(2，m)可作曲线y＝f(x)的三条切线，求实数m的取值范围．

【解析】本试题主要考查了导数在研究函数中的运用。第一问，利用函数f(x)＝ax³＋bx²＋cx在x＝±1处取得极值，且在x＝0处的切线的斜率为－3，得到c＝－3　∴a＝1, f(x)＝x³－3x

(2)中设切点为(x₀，x₀³－3x₀)，因为过点A(2，m)，所以∴m－(x₀³－3x₀)＝(3x₀²－3)(2－x₀)分离参数∴m＝－2x₀³＋6x₀²－6

然后利用g(x)＝－2x³＋6x²－6函数求导数，判定单调性，从而得到要是有三解，则需要满足－6<m<2

解：(1)f′(x)＝3ax²＋2bx＋c

依题意

又f′(0)＝－3

∴c＝－3　∴a＝1　∴f(x)＝x³－3x

(2)设切点为(x₀，x₀³－3x₀)，

∵f′(x)＝3x²－3，∴f′(x₀)＝3x₀²－3

∴切线方程为y－(x₀³－3x₀)＝(3x₀²－3)(x－x₀)

又切线过点A(2，m)

∴m－(x₀³－3x₀)＝(3x₀²－3)(2－x₀)

∴m＝－2x₀³＋6x₀²－6

令g(x)＝－2x³＋6x²－6

则g′(x)＝－6x²＋12x＝－6x(x－2)

由g′(x)＝0得x＝0或x＝2

∴g(x)在(－∞，0)单调递减，(0,2)单调递增，(2，＋∞)单调递减．

∴g(x)_极小值＝g(0)＝－6，g(x)_极大值＝g(2)＝2

画出草图知，当－6<m<2时，m＝－2x³＋6x²－6有三解，

所以m的取值范围是(－6,2)．