
题目列表(包括答案和解析)
如图2所示,一带电粒子以水平初速度![]() (
(![]() )先后进入方向垂直的匀强电场和匀强磁场区域,已知电场方向竖直向宽度相同且紧邻在一起,在带电粒子穿过电场和磁场的过程中(其所受重力忽略不计),电场和磁场对粒子所做的总功为
)先后进入方向垂直的匀强电场和匀强磁场区域,已知电场方向竖直向宽度相同且紧邻在一起,在带电粒子穿过电场和磁场的过程中(其所受重力忽略不计),电场和磁场对粒子所做的总功为![]() ;若把电场和磁场正交重叠,如图3所示,粒子仍以初速度
;若把电场和磁场正交重叠,如图3所示,粒子仍以初速度![]() 穿过重叠场区,在带电粒子穿过电场和磁场的过程中,电场和磁场对粒子所做的总功为
穿过重叠场区,在带电粒子穿过电场和磁场的过程中,电场和磁场对粒子所做的总功为![]() ,比较
,比较![]() 和
和![]() ,有( )
,有( )
A.一定是![]() B.一定是
B.一定是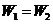
C.一定是![]() D.可能是
D.可能是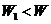 ,也可能是
,也可能是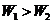
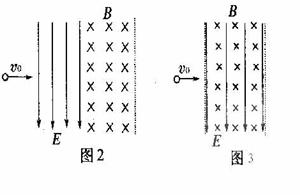
如图2所示,一带电粒子以水平初速度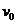 (
(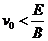 )先后进入方向垂直的匀强电场和匀强磁场区域,已知电场方向竖直向宽度相同且紧邻在一起,在带电粒子穿过电场和磁场的过程中(其所受重力忽略不计),电场和磁场对粒子所做的总功为
)先后进入方向垂直的匀强电场和匀强磁场区域,已知电场方向竖直向宽度相同且紧邻在一起,在带电粒子穿过电场和磁场的过程中(其所受重力忽略不计),电场和磁场对粒子所做的总功为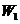 ;若把电场和磁场正交重叠,如图3所示,粒子仍以初速度
;若把电场和磁场正交重叠,如图3所示,粒子仍以初速度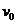 穿过重叠场区,在带电粒子穿过电场和磁场的过程中,电场和磁场对粒子所做的总功为
穿过重叠场区,在带电粒子穿过电场和磁场的过程中,电场和磁场对粒子所做的总功为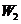 ,比较
,比较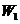 和
和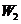 ,有( )
,有( )
A.一定是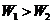 B.一定是
B.一定是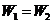
C.一定是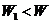 D.可能是
D.可能是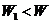 ,也可能是
,也可能是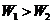
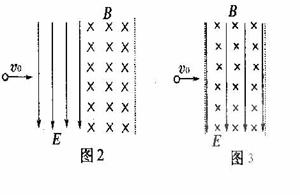
如图1所示,一带电粒子以水平速度v0(v0<E/B)先后进入方向互相垂直的匀强电场和匀强磁场区域,已知电场方向竖直向下,两个区域的宽度相同且紧邻在一起,在带电粒子穿过电场和磁场的过程中,(其所受重力忽略不计),电场和磁场对粒子所做的功为W1;若把电场和磁场正交重叠,如图2所示,粒子仍以初速度v0穿过重叠场区,在带电粒子穿过电场和磁场的过程中,电场和磁场对粒子所做的总功为W2,比较W1和W2,则
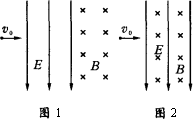
A.一定是W1>W2
B.一定是W1=W2
C.一定是W1<W2
D.可能是W1<W2,也可能是W1>W2
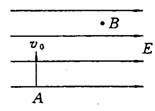
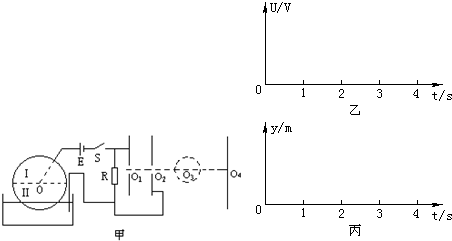 如图甲所示,一个半径r=10cm圆盘由两种材料Ⅰ、Ⅱ构成,每种材料正好形成一个半圆,它们之间除圆心O以外由绝缘薄膜隔开.圆盘下端浸没在导电液体中,O点到液面的距离是半径r的
如图甲所示,一个半径r=10cm圆盘由两种材料Ⅰ、Ⅱ构成,每种材料正好形成一个半圆,它们之间除圆心O以外由绝缘薄膜隔开.圆盘下端浸没在导电液体中,O点到液面的距离是半径r的
| ||
| 2 |
| q |
| m |
| 2 |
| 3 |
1. BCD 2. BC 3.D 4.A 5. C
6. AD 7.C 8. CD 9. AB 10.BC
11.(1)CD(2)指零 指零 指零 左偏
12. 电极A与导电纸接触不良
13. 解:(1)小球速度最大时,棒对它的弹力垂直于棒向下,受力分析如图,沿杆方向,电磁学中的“场”.files/image242.gif) ,垂直杆方向:
,垂直杆方向:电磁学中的“场”.files/image244.gif) ,
,电磁学中的“场”.files/image246.gif) 联立以上各式,得
联立以上各式,得电磁学中的“场”.files/image248.gif)
所以:电磁学中的“场”.files/image250.gif)
(2)小球C从斜置的绝缘棒上由静止开始运动,必须满足条件电磁学中的“场”.files/image252.gif) ,而
,而电磁学中的“场”.files/image254.gif) 即
即电磁学中的“场”.files/image256.gif) ,所以
,所以电磁学中的“场”.files/image258.gif)
14. 解:(1)根据牛顿第二定律电磁学中的“场”.files/image260.gif) ,根据库仑定律
,根据库仑定律电磁学中的“场”.files/image262.gif) ,
,电磁学中的“场”.files/image264.gif) ,解得
,解得电磁学中的“场”.files/image266.gif)
(2)当A球受到的合力为零即加速度为零时,动能最大,设此时A球与B点间的距离为R,则电磁学中的“场”.files/image268.gif) ,解得
,解得电磁学中的“场”.files/image270.gif) 。
。
15. 解:(1)、(2)如图所示,设小球在C点的速度大小是电磁学中的“场”.files/image272.gif) ,对轨道的压力大小为
,对轨道的压力大小为电磁学中的“场”.files/image274.gif) ,则对于小球由A
,则对于小球由A电磁学中的“场”.files/image276.gif) C的过程中,应用动能定理列出:
C的过程中,应用动能定理列出:电磁学中的“场”.files/image278.gif) -0,在C点的园轨道径向应用牛顿第二定律,有
-0,在C点的园轨道径向应用牛顿第二定律,有电磁学中的“场”.files/image280.gif) ,解得
,解得电磁学中的“场”.files/image282.gif)
(3)如图所示,设小球初始位置应在离B点xm的电磁学中的“场”.files/image284.gif) 点,对小球由
点,对小球由电磁学中的“场”.files/image284.gif)
电磁学中的“场”.files/image276.gif) D的过程应用动能定理,有:
D的过程应用动能定理,有:电磁学中的“场”.files/image287.gif) ,在D点的圆轨道径向应用牛顿第二定律,有
,在D点的圆轨道径向应用牛顿第二定律,有电磁学中的“场”.files/image289.gif) ,解得
,解得电磁学中的“场”.files/image291.gif)
16. 解:(1)F1为P1参与的运动而受到指向N端的洛伦兹力,其值为:电磁学中的“场”.files/image293.gif) (其中
(其中 电磁学中的“场”.files/image295.gif) ,为
,为电磁学中的“场”.files/image297.gif) 的电量),
的电量),电磁学中的“场”.files/image297.gif) 对应有指向N端的加速度:
对应有指向N端的加速度:电磁学中的“场”.files/image300.gif) (其中m为
(其中m为电磁学中的“场”.files/image297.gif) 的质量)
的质量)
电磁学中的“场”.files/image297.gif) 在管中运动会使它受到另一个向左的洛伦兹力,此力与管壁对
在管中运动会使它受到另一个向左的洛伦兹力,此力与管壁对电磁学中的“场”.files/image297.gif) 向右的力所抵消,
向右的力所抵消,电磁学中的“场”.files/image297.gif) 到达N端时具有沿管长方向的速度:
到达N端时具有沿管长方向的速度:电磁学中的“场”.files/image302.gif)
所以,电磁学中的“场”.files/image297.gif) 对纸平面的速度大小为:
对纸平面的速度大小为: 电磁学中的“场”.files/image304.gif)
又因为电磁学中的“场”.files/image306.gif) ,故:
,故:电磁学中的“场”.files/image308.gif)
即:电磁学中的“场”.files/image310.gif)
所以电磁学中的“场”.files/image297.gif) 的比荷为:
的比荷为:电磁学中的“场”.files/image312.gif)
(2)电磁学中的“场”.files/image297.gif) 从M端到N端经历的时间为:
从M端到N端经历的时间为:电磁学中的“场”.files/image314.gif)
电磁学中的“场”.files/image297.gif) 离开管后将在纸平面上做匀速圆周运动,半径与周期分别为:
离开管后将在纸平面上做匀速圆周运动,半径与周期分别为:电磁学中的“场”.files/image316.gif)
电磁学中的“场”.files/image318.gif)
电磁学中的“场”.files/image297.gif) 经t1时间已随管朝正右方向运动:
经t1时间已随管朝正右方向运动:电磁学中的“场”.files/image320.gif)
的距离
所以电磁学中的“场”.files/image297.gif) 离开N端的位置恰好为
离开N端的位置恰好为电磁学中的“场”.files/image322.gif) 的初始位置
的初始位置
电磁学中的“场”.files/image322.gif) 经时间t1已知运动到如图所示的位置S2走过的路程为
经时间t1已知运动到如图所示的位置S2走过的路程为电磁学中的“场”.files/image325.gif)
电磁学中的“场”.files/image297.gif) 只能与
只能与电磁学中的“场”.files/image322.gif) 相碰在图中的S处,相遇时刻必为
相碰在图中的S处,相遇时刻必为
电磁学中的“场”.files/image327.gif)
且要求电磁学中的“场”.files/image322.gif) 在这段时间内恰好走过2R的路程,因此有
在这段时间内恰好走过2R的路程,因此有
电磁学中的“场”.files/image329.gif)
即得:电磁学中的“场”.files/image331.gif)
所以:电磁学中的“场”.files/image333.gif)
17. 解:电磁学中的“场”.files/image335.gif) ……①
……① 电磁学中的“场”.files/image337.gif)
由于重力和电场力平衡,电粒子在洛伦兹力作用下做圆周运动,小球平抛且碰时动量守恒,根据条件,碰后电磁学中的“场”.files/image339.gif) 反向
反向
电磁学中的“场”.files/image341.gif) ……①
……①
另有电磁学中的“场”.files/image343.gif) ……②
……②
解得电磁学中的“场”.files/image345.gif) ……③
……③
对平抛:电磁学中的“场”.files/image347.gif)
解得电磁学中的“场”.files/image349.gif)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com