
题目列表(包括答案和解析)
(14分)核聚变能以氘、氚等为燃料,具有安全、洁净、资源无限三大优点,是最终解决人类能源危机的最有效手段。
(1)两个氘核![]() 结合成一个氦核
结合成一个氦核![]() 时,要放出某种粒子,同时释放出能量,写出核反应的方程。若氘核的质量为m1, 氦核的质量为m2,所放出粒子的质量为m3,求这个核反应中释放出的能量为多少?
时,要放出某种粒子,同时释放出能量,写出核反应的方程。若氘核的质量为m1, 氦核的质量为m2,所放出粒子的质量为m3,求这个核反应中释放出的能量为多少?
(2)要使两个氘核能够发生聚变反应,必须使它们以巨大的速度冲破库仑斥力而碰到一起,已知当两个氘核恰好能够彼此接触发生聚变时,它们的电势能为![]() (其中e为氘核的电量,R为氘核半径,
(其中e为氘核的电量,R为氘核半径,![]() 为介电常数,均为已知),则两个相距较远(可认为电势能为零)的等速氘核,至少具有多大的速度才能在相向运动后碰在一起而发生聚变?
为介电常数,均为已知),则两个相距较远(可认为电势能为零)的等速氘核,至少具有多大的速度才能在相向运动后碰在一起而发生聚变?

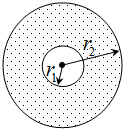
(3)当将氘核加热成几百万度的等离子状态时就可以使其获得所需速度。有一种用磁场来“约束”高温等离子体的装置叫做“托卡马克”,如图所示为其“约束”原理图:两个同心圆的半径分别为r1和r2,等离子体只在半径为r1的圆形区域内反应,两圆之间的环形区内存在着垂直于截面的匀强磁场。为保证速率为v的氘核从反应区进入磁场后不能从磁场区域的外边界射出,所加磁场磁感应强度的最小值为多少?(不考虑速度大小对氘核质量的影响)
(18分)近代的材料生长和微加工技术,可制造出一种使电子的运动限制在半导体的一个平面内(二维)的微结构器件,且可做到电子在器件中像子弹一样飞行,不受杂质原子射散的影响,这种特点可望有新的应用价值。图l 所示为四端十字形。二维电子气半导体,当电流从l端进人时,通过控制磁场的作用,可使电流从 2,3或4端流出。对下面摸拟结构的研究,有助于理解电流在上述四端十字形导体中的流动。在图 2 中, a、b、c、d为四根半径都为R的圆柱体的横截面,彼此靠得很近,形成四个宽度极窄的狭缝1、2、3、4,在这些狭缝和四个圆柱所包围的空间(设为真空)存在匀强磁场,磁场方向垂直于纸面指向纸里。以B表示磁感应强度的大小。一个质量为m、电荷量为q的带正电的粒子,在纸面内以速度v0沿与a、b都相切的方向由缝1射人磁场内,设粒子与圆柱表面只发生一次碰撞,碰撞是弹性的,碰撞时间极短,且碰撞不改变粒子的电荷量,也不受摩擦力作用。试求B为何值时,该粒子能从缝2处且沿与b、c都相切的方向射出。

| 21 |
| 32 |
| e2 |
| 4πε0(2R) |
 (2009?天津模拟)核聚变能以氘、氚等为燃料,具有安全、洁净、储量丰富三大优点,是最终解决人类能源危机的最有效手段.
(2009?天津模拟)核聚变能以氘、氚等为燃料,具有安全、洁净、储量丰富三大优点,是最终解决人类能源危机的最有效手段.2 1 |
3 2 |
| e2 |
| 4πε0(2R) |
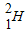 结合成一个氦核
结合成一个氦核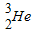 时,要放出某种粒子,同时释放出能量,写出核反应的方程.若氘核的质量为m1,氦核的质量为m2,所放出粒子的质量为m3,求这个核反应中释放出的能量为多少?
时,要放出某种粒子,同时释放出能量,写出核反应的方程.若氘核的质量为m1,氦核的质量为m2,所放出粒子的质量为m3,求这个核反应中释放出的能量为多少? (其中e为氘核的电量,R为氘核半径,ε为介电常数,均为已知),则两个相距较远(可认为电势能为零)的等速氘核,至少具有多大的速度才能在相向运动后碰在一起而发生聚变?
(其中e为氘核的电量,R为氘核半径,ε为介电常数,均为已知),则两个相距较远(可认为电势能为零)的等速氘核,至少具有多大的速度才能在相向运动后碰在一起而发生聚变?
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com