
题目列表(包括答案和解析)
从以下两个小题中选做一题(只能做其中一个,做两个按得分最低的记分).(甲)一水池有2个进水口,1个出水口,每口进出水速度如图甲、乙所示.某天0点到6点,该水池的蓄水量如图丙所示.(至少打开一个水口)

给出以下3个论断:①0点到3点只进水不出水;②3点到4点不进水只出水;③4点到6点不进水不出水.则一定能确定正确的论断序号是________.
(乙)深圳市的一种特色水果上市时间仅能持续5个月,预测上市初期和后期会因供不应求使价格呈连续上涨态势,而中期又将出现供大于求使价格连续下跌,现有三种价格模拟函数.①f(x)p·qx;②f(x)=px2+qx+1;③f(x)=x(x-q)2+p
(以上三式中p,q均为常数,且q>1,x=0表示4月1日,x=1表示5月1日,依次类推).
(1)为准确研究其价格走势,应选________种价格模拟函数.
(2)若f(x)=4,f(2)=6,预测该果品在________月份内价格下跌.
有下列命题:
①;到两个定点 距离的和等于定长的点的轨迹是椭圆;
距离的和等于定长的点的轨迹是椭圆;
②命题“若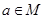 ,则
,则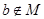 ”的逆否命题是:若
”的逆否命题是:若 ;
;
③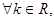 曲线
曲线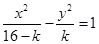 表示双曲线
表示双曲线
④设集合M = {x | 0< x ≤3},N = {x | 0< x ≤2},则“a∈M”是“a∈N”的充分而不必要条件则上述命题中真命题为 (填上序号)
现给出如下命题:
(1)若直线 上有两个点到平面
上有两个点到平面 的距离相等,则直线
的距离相等,则直线 ;
;
(2)“平面 上有四个不共线的点到平面
上有四个不共线的点到平面 的距离相等”的充要条件是“平面
的距离相等”的充要条件是“平面 ”;
”;
(3)若一个球的表面积是 ,则它的体积
,则它的体积 ;
;
(4)若从总体中随机抽取的样本为 ,则该总体均值的点估计值是
,则该总体均值的点估计值是 .则其中正确命题的序号是
( )
.则其中正确命题的序号是
( )
A.(1)、(2)、(3). B.(1)、(2)、(4). C.(3)、(4). D.(2)、(3).
 距离的和等于定长的点的轨迹是椭圆;
距离的和等于定长的点的轨迹是椭圆;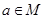 ,则
,则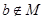 ”的逆否命题是:若
”的逆否命题是:若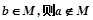 ;
;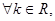 曲线
曲线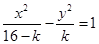 表示双曲线
表示双曲线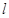 上有两个点到平面
上有两个点到平面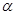 的距离相等,则直线
的距离相等,则直线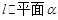 ;
;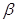 上有四个不共线的点到平面
上有四个不共线的点到平面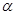 的距离相等”的充要条件是“平面
的距离相等”的充要条件是“平面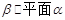 ”;
”;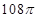 ,则它的体积
,则它的体积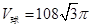 ;
;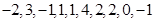 ,则该总体均值的点估计值是
,则该总体均值的点估计值是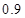 .则其中正确命题的序号是 ( )
.则其中正确命题的序号是 ( )| A.(1)、(2)、(3). | B.(1)、(2)、(4). | C.(3)、(4). | D.(2)、(3). |
一、填空题
1、--数学.files/image125.gif) 2、40 3、②
④) 4、-1 5、
2、40 3、②
④) 4、-1 5、--数学.files/image127.gif) 6、3
6、3
7、--数学.files/image129.gif) 8、
8、--数学.files/image131.gif) 9、1 10、
9、1 10、--数学.files/image133.gif) 11、
11、--数学.files/image135.gif) 12、46
12、46
13、解:(1)∵a⊥b,∴a?b=0.而a=(3sinα,cosα),b=(2sinα, 5sinα-4cosα),
故a?b=6sin2α+5sinαcosα-4cos2α=0.……………………………………2分
由于cosα≠0,∴6tan2α+5tanα-4 =0.解之,得tanα=---数学.files/image137.gif) ,或tanα=
,或tanα=--数学.files/image139.gif) .……… 6分
.……… 6分
∵α∈(--数学.files/image104.gif) ),tanα<0,故tanα=
),tanα<0,故tanα=--数学.files/image139.gif) (舍去).∴tanα=-
(舍去).∴tanα=---数学.files/image137.gif) .…………7分
.…………7分
(2)∵α∈(--数学.files/image104.gif) ),∴
),∴--数学.files/image141.gif) .
.
由tanα=---数学.files/image137.gif) ,求得
,求得--数学.files/image143.gif) ,
,--数学.files/image145.gif) =2(舍去).
=2(舍去).
∴--数学.files/image147.gif) ,…………………………………………………………12分
,…………………………………………………………12分
cos(--数学.files/image149.gif) )=
)=--数学.files/image151.gif) =
=--数学.files/image153.gif) =
=--数学.files/image155.gif) . ……15分
. ……15分
14、解:由已知圆的方程为--数学.files/image157.gif) ,
,
按--数学.files/image159.gif) 平移得到
平移得到--数学.files/image161.gif) .
.
∵--数学.files/image163.gif) ∴
∴--数学.files/image165.gif) .
.
即--数学.files/image167.gif) .
.
又--数学.files/image169.gif) ,且
,且--数学.files/image159.gif) ,∴
,∴--数学.files/image172.gif) .∴
.∴--数学.files/image174.gif) .
.
设--数学.files/image176.gif) ,
, --数学.files/image178.gif) 的中点为D.
的中点为D.
由--数学.files/image180.gif) ,则
,则--数学.files/image182.gif) ,又
,又--数学.files/image184.gif) .
.
∴--数学.files/image186.gif) 到
到--数学.files/image188.gif) 的距离等于
的距离等于--数学.files/image190.gif) . 即
. 即--数学.files/image192.gif) , ∴
, ∴--数学.files/image194.gif) .
.
∴直线--数学.files/image113.gif) 的方程为:
的方程为:--数学.files/image197.gif) 或
或--数学.files/image199.gif) .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com