
题目列表(包括答案和解析)
(本小题满分12分)
如图,以原点O为顶点,以y轴为对称轴的抛物线E的焦点为F(0,1),点M是直线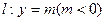 上任意一点,过点M引抛物线E的两条切线分别交x轴于点S , T,切点分别为B、A。
上任意一点,过点M引抛物线E的两条切线分别交x轴于点S , T,切点分别为B、A。
(1)求抛物线E的方程;
(2)求证:点S,T在以FM为直径的圆上;
(3)当点M在直线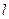 上移动时,直线AB恒过焦点F,求
上移动时,直线AB恒过焦点F,求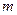 的值。
的值。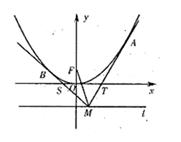
(本小题满分12分)已知抛物线 的焦点为F,过点F作直线
的焦点为F,过点F作直线 与抛物线交于A,B两点,抛物线的准线与
与抛物线交于A,B两点,抛物线的准线与 轴交于点C。
轴交于点C。
(1)证明: ;
;
(2)求 的最大值,并求
的最大值,并求 取得最大值时线段AB的长。
取得最大值时线段AB的长。
(本小题满分12分)
设抛物线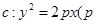 >0)上有两动点A、B(AB不垂直
>0)上有两动点A、B(AB不垂直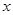 轴),F为焦点,且
轴),F为焦点,且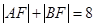 ,又线段AB的垂直平分线经过定点Q(6,0),求抛物线方程。
,又线段AB的垂直平分线经过定点Q(6,0),求抛物线方程。
(本小题满分12分)
如图,斜率为1的直线过抛物线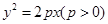 的焦点,与抛物线交于两点A、B,将直线AB按向量
的焦点,与抛物线交于两点A、B,将直线AB按向量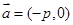 平移得直线
平移得直线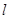 ,N为
,N为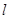 上的动点。
上的动点。
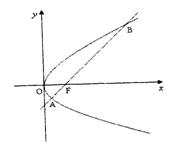
(1)若|AB|=8,求抛物线的方程;
(2)求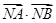 的最小值。
的最小值。
(本小题满分12分)
已知椭圆 的两焦点与短轴的一个端点的连线构成等腰直角三角形,直线
的两焦点与短轴的一个端点的连线构成等腰直角三角形,直线 是抛物线
是抛物线 的一条切线.
的一条切线.
(Ⅰ)求椭圆的方程;
(Ⅱ)过点 的动直线L交椭圆C于A.B两点.问:是否存在一个定点T,使得以AB为直径的圆恒过点T ? 若存在,求点T坐标;若不存在,说明理由.
的动直线L交椭圆C于A.B两点.问:是否存在一个定点T,使得以AB为直径的圆恒过点T ? 若存在,求点T坐标;若不存在,说明理由.
一、选择题
题号
1
2
3
4
5
6
7
8
9
10
11
12
答案
C
A
B
D
D
C
D
C
C
D
B
C
|