
可得:在△PAB中,PA2+AB2=PB2=6。
所以PA⊥AB
同理可证PA⊥AD
故PA⊥平面ABCD (4分)
(2)取PE中点M,连接FM,BM,
连接BD交AC于O,连接OE
∵F,M分别是PC,PF的中点,
∴FM∥CE,
又FM 面AEC,CE
面AEC,CE 面AEC
面AEC
∴FM∥面AEC
又E是DM的中点
OE∥BM,OE 面AEC,BM
面AEC,BM 面AEC
面AEC
∴BM∥面AEC且BM∩FM=M
∴平面BFM∥平面ACE
又BF 平面BFM,∴BF∥平面ACE (4分)
平面BFM,∴BF∥平面ACE (4分)
(3)连接FO,则FO∥PA,因为PA⊥平面ABCD,则FO⊥平面ABCD,所以FO=1,
SㄓACD=1,
∴VFACD=VF――ACD= (4分)
(4分)
19. (1)由已知圆的标准方程为:(x-aCosφ)2+(y-aSinφ)2=a2(a>0)
设圆的圆心坐标为(x,y),则 (
( 为参数),
为参数),
消参数得圆心的轨迹方程为:x2+y2=a2,…………(5分)
(2)有方程组 得公共弦的方程:
得公共弦的方程:
 圆X2+Y2=a2的圆心到公共弦的距离d=
圆X2+Y2=a2的圆心到公共弦的距离d= ,(定值)
,(定值)
∴弦长l= (定值)
(5分)
(定值)
(5分)
20.解:(1) ,
,
 当
当 时,
时, 取最小值
取最小值 ,
,
即 .(6分)
.(6分)
(2)令 ,
,
由 得
得 ,
, (不合题意,舍去).
(不合题意,舍去).
当 变化时
变化时 ,
, 的变化情况如下表:
的变化情况如下表:









递增
极大值
递减
 在
在 内有最大值
内有最大值 .
.
 在
在 内恒成立等价于
内恒成立等价于 在
在 内恒成立,
内恒成立,
即等价于 ,
,
所以 的取值范围为
的取值范围为 .(6分)
.(6分)
21.解:(1) ,
,
 ,
, .
.
又 ,
,
 数列
数列 是首项为
是首项为 ,公比为
,公比为 的等比数列,
的等比数列, .
.
当 时,
时, ,
,
 (6分)
(6分)
(2) ,
,
当 时,
时, ;
;
当 时,
时, ,…………①
,…………①
 ,………………………②
,………………………②
 得:
得:

 .
.
 .
.
又 也满足上式,
也满足上式,
 .(6分)
.(6分)
22.解:(1)由题意椭圆的离心率



∴椭圆方程为 ……2分
……2分
又点 在椭圆上
在椭圆上

 ∴椭圆的方程为
∴椭圆的方程为 (4分)
(4分)
(2)设
由
消去 并整理得
并整理得 ……6分
……6分
∵直线 与椭圆有两个交点
与椭圆有两个交点
 ,即
,即 ……8分
……8分
又
 中点
中点 的坐标为
的坐标为 ……10分
……10分
设 的垂直平分线
的垂直平分线 方程:
方程:
 在
在 上
上

即
 ……12分
……12分
将上式代入得
 即
即 或
或
 的取值范围为
的取值范围为 …………(8分)
…………(8分)

![]() 等于
等于 ![]() 等于
等于 ![]() 等于
等于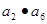 等于(
)
等于(
) 等于(
)
等于(
)