
题目列表(包括答案和解析)
设![]() ,O为坐标原点,若A、B、C三点共线,则
,O为坐标原点,若A、B、C三点共线,则![]() 的最小值是
的最小值是
A.2 B.4 C.6 D.8
| a |
| b |
设![]() ,a>0,b>0,O为坐标原点,若A、B、C三点共线,则
,a>0,b>0,O为坐标原点,若A、B、C三点共线,则![]() 的最小值是
的最小值是
A.2
B.4
C.6
D.8
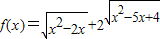 的最小值为l+2
的最小值为l+2 ;
; ,且|x1|>|x2|时,有f (x1)>f(x2)”是真命题;
,且|x1|>|x2|时,有f (x1)>f(x2)”是真命题; ”是函数“y=cos2(ax)-sin2(ax)的最小正周期为4”的充要条件;
”是函数“y=cos2(ax)-sin2(ax)的最小正周期为4”的充要条件; 为不共线向量,又
为不共线向量,又 ,若
,若 ,则S2012=2013.
,则S2012=2013.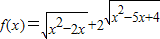 的最小值为l+2
的最小值为l+2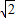 ;
; ,且|x1|>|x2|时,有f (x1)>f(x2)”是真命题;
,且|x1|>|x2|时,有f (x1)>f(x2)”是真命题;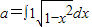 ”是函数“y=cos2(ax)-sin2(ax)的最小正周期为4”的充要条件;
”是函数“y=cos2(ax)-sin2(ax)的最小正周期为4”的充要条件;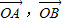 为不共线向量,又
为不共线向量,又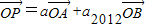 ,若
,若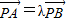 ,则S2012=2013.
,则S2012=2013.一、选择题:(每题5分,共60分)
|