练习册

  • 练习册
  • 试题
    2． 答卷前将密封线内的项目填写清楚.得 分评卷人 【查看更多】

     

    题目列表(包括答案和解析)

    （2008•成都二模）（新华网）反兴奋剂的大敌、服药者的宠儿--HGH（人体生长激素），有望在8月的北京奥运会上首次“伏法”．据悉，国际体育界研究近10年仍不见显著成效的HGH检测，日前已取得新的进展，新生产的检测设备有希望在北京奥运会上使用．若组委会计划对参加某项田径比赛的120名运动员的血样进行突击检查，采用如下化验
    方法：将所有待检运动员分成若干小组，每组m个人，再把每个人的血样分成两份，化验时将每个小组内的m个人的血样各一份混合在一起进行化验，若结果中不含HGH成分，那么该组的m个人只需化验这一次就算检验合格；如果结果中含有HGH成分，那么需要对该组进行再次检验，即需要把这m个人的另一份血样逐个进行化验，才能最终确定是否检验合格，这时，对这m个人一共需要进行m+1次化验．假定对所有人来说，化验结果中含有HGH成分的概率均为
    110
    ．当m=3时，
    （1）求一个小组只需经过一次检验就合格的概率；
    （2）设一个小组的检验次数为随机变量ξ，求ξ的分布列及数学期望．

    查看答案和解析>>

    如图是将二进制数11111（2）化为十进制数的一个程序框图．
    （1）将判断框内的条件补充完整；
    （2）请用直到型循环结构改写流程图．

    查看答案和解析>>

    组委会计划对参加某项田径比赛的12名运动员的血样进行突击检验，检查是否含有兴奋剂HGH成分．采用如下检测方法：将所有待检运动员分成4个小组，每组3个人，再把每个人的血样分成两份，化验室将每个小组内的3个人的血样各一份混合在一起进行化验，若结果中不含HGH成分，那么该组的3个人只需化验这一次就算合格；如果结果中含HGH成分，那么需对该组进行再次检验，即需要把这3个人的另一份血样逐个进行化验，才能最终确定是否检验合格，这时，对这3个人一共进行了4次化验，假定对所有人来说，化验结果中含有HGH成分的概率均为
    110
    ．
    （Ⅰ）求一个小组只需经过一次检验就合格的概率；
    （Ⅱ）设一个小组检验次数为随机变量ξ，求ξ的分布列及数学期望；
    （Ⅲ）至少有两个小组只需经过一次检验就合格的概率．（精确到0.01，参考数据：0.2713≈0.020，0.2714≈0.005，0.7292≈0.500）

    查看答案和解析>>

    ．假定平面内的一条直线将该平面内的一个区域分成面积相等的两个区域，则称这条直线平分这个区域．如图，是平面内的任意一个封闭区域．现给出如下结论：

             ① 过平面内的任意一点至少存在一条直线平分区域；

             ②过平面内的任意一点至多存在一条直线平分区域；

             ③ 过区域内的任意一点至少存在两条直线平分区域；

    ④ 过区域内的某一点可能存在无数条直线平分区域．

             其中结论正确的是

           A．①③                              B．①④                              C．②③                              D．③④

     

    查看答案和解析>>

    假定平面内的一条直线将该平面内的一个区域分成面积相等的两个区域，则称这条直线平分这个区域．如图，是平面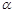内的任意一个封闭区域.现给出如下结论：

    ①        过平面内的任意一点至少存在一条直线平分区域；

    ②        过平面内的任意一点至多存在一条直线平分区域；

    ③        区域内的任意一点至少存在两条直线平分区域；

    ④        平面内存在互相垂直的两条直线平分区域成四份．

    其中正确结论的序号是               ．

     

    查看答案和解析>>

    一、选择题：本大题共10小题，每小题5分，共50分。在每小题给出的四个选项中，只有 一项是符合题目要求的。

    1．B  2．D 3．B  4．C  5．C  6．B  7．A  8．B  9．A  10．D

     

    二、填空题：本大题共5个小题，每小题5分，共25分，把答案填在题中的横线上。

    11.6  12．2   13．80  14．20  15． 0，

    三、解答题：本大题共6小题，共75分。解答应写文字说明，证明过程或演算步骤。

    16．解(1)证明:由得

    ∴………………………………………………4分

    (2)由正弦定理得     ∴……① …………6分

      又,=2,       ∴ …………② …………8分

    解①②得 ,           …………………………………………10分

    ∴                          …………………12分

    17．解:(1)由得,即=0.……………2分

    当n>2时有

       ∴                        ……………………………6分

    (2)由(1)知n>2时,……………8分

    又=0,  =2也适合上式,

    ∴   ∴……………………10分

    ∴

                      =1-<1……………………………………………12分

     

    18．解：（1）分别取BE、AB的中点M、N，

    连结PM、MC，PN、NC,则PM=1，MB=，BC=，

    ∴MC=，而PN=MB=，

    NC=，∴PC=，…………………………4分

    ∴

    故所求PC与AB所成角的余弦值为………6分

    （2）连结AP，∵二面角E-AB-C是直二面角，且AC⊥AB

    ∴∠BAP即为所求二面角的平面角，即∠BAP=300……8分

    在RtΔBAF中，tan∠ABF=，∴∠ABF=600，

    故BF⊥AP，    ………………………………………10分

    又AC⊥面BF，∴BF⊥AC，故BF⊥平面PAC………12分

    另解：分别以AB、AC、AF为x、y、z轴建立直角坐标系，

    则，

      ∴

    而，  ∴

    故异面直线PC与AB所成的角的余弦值为

    （2）分别设平面ABC和平面PAC的法向量分别为，P点坐标设为，则而，则由

    得

    且 ∴，

    再由得

    ∴，，

    而

    ∴，即

    BF⊥AP，BF⊥AC∴BF⊥平面PAC

     

    19．解：（1）当0<x≤10时，……2分

    当x >10时，…………4分

    …………………………………5分

    （2）①当0<x≤10时，由

    当

    ∴当x=9时，W取最大值，且……9分

    ②当x>10时，W=98

    当且仅当…………………………12分

    综合①、②知x=9时，W取最大值.

    所以当年产量为9千件时，该公司在这一品牌服装生产中获利最大.……13分

    20． 解: （I） ,依题意有:,…………………2分

                即,

             ,由

              (也可写成闭区间)……………4分

    （2）   (1)

         函数的图象与直线的交点的个数问题可转化为方程(1)的解的个数问题.

           令

    则…………………………5分

    ①6分

    ②

     

       ……………………9分

    ③

    ∴的极大值为

    ∴的图象与轴只有一个交点.…………………………………12分

    综上所述: ;

    .……………13分

     

    21．解：（1）B（0，-b）

    ,即D为线段FP的中点.

    ∴ ……………………………2分

    ,即A、B、D共线.

    而 

    ∴,得,

    ∴………………………………………5分

     

    （2）∵=2,而,∴,故双曲线的方程为………①

    ∴B、的坐标为(0,-1)…………………………………………………………6分

    假设存在定点C（0，）使为常数.

    设MN的方程为………………②

    ②代入①得………………………………………7分

    由题意得:   得:……8分

    设M、N的坐标分别为(x1,y1) 、(x2,y2)

         …………………………………………………………9分

    而=

             =

    ==,…………………………10分

    整理得:

    对满足的恒成立.

    ∴且

    解得

    存在轴上的定点C(0,4),使为常数17.…………………………13分

     

     


    同步练习册答案