练习册

  • 练习册
  • 试题
    20．在东西方向直线延伸的湖岸上有一港口O.一艘机艇以40km/h的速度从O港出发.先沿东偏北的某个方向直线前进到达A处.然后改向正北方向航行.总共航行30分钟因机器出现故障而停在湖里的P处.由于营救人员不知该机艇的最初航向及何时改变的航向.故无法确定机艇停泊的准确位置.试划定一个最佳的弓形营救区域.并说明你的理由. 【查看更多】

     

    题目列表(包括答案和解析)

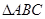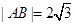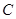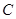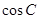    (本小题满分14分）在周长为定值的中，已知，动点的运动轨迹为曲线G,且当动点运动时，有最小值.

    (1)以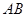所在直线为轴，线段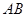的中垂线为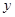轴建立直角坐标系，求曲线G的方程.

    (2)过点(m,0)作圆x2＋y2＝1的切线l交曲线G于M，N两点．将线段MN的长|MN|表示为m的函数，并求|MN|的最大值．

     

    查看答案和解析>>

    （本小题满分14分）

        在

       （I）求的值；

       （II）求的值.

     

    查看答案和解析>>

    （本小题满分14分） 在平面上有一系列的点, 对于正整数，点位于函数的图像上，以点为圆心的与轴相切，且与又彼此外切，若，且（1）求证：数列是等差数列；（2）设的面积为，求证： 

    查看答案和解析>>

    （本小题满分14分）

      在棱长为2的正方体ABCD—A1B1C1D1中，E，F分别为A1D1和CC1的中点．

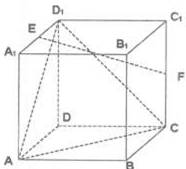
    （Ⅰ）求证：EF//平面ACD1；

    （Ⅱ）求异面直线EF与AB所成的角的余弦值；

    （Ⅲ）在棱BB1上是否存在一点P，使得二面角P—AC—B的大小为30°？若存在，求出BP的长；若不存在，请说明理由．

     

    查看答案和解析>>

    （本小题满分14分）在△中，所对的边分别为，向量，其中且，已知 ,.（Ⅰ）求（Ⅱ）若,求、.

    查看答案和解析>>

    一．选择题：CADDC  CBCAC

    解析：1.解：，，则集合B中必含有元素3，即此题可转化为求集合的子集个数问题，所以满足题目条件的集合B共有个。故选择答案C。

    2．只要注意到，即可迅速得到答案.

    3.特殊值法, 令, 得.

    4.应注意到函数是奇函数, 可排除A, B选项, 代数值检验即得D.

    5.可理解为首项是，公差是的等差数列，故

    6.由题意知同族函数的定义域非空, 且由中的两个(这里和中各有一个), 或三个, 或全部元素组成, 故定义域的个数为.

    7.设签字笔与笔记本的价格分别是, 2支签字笔与3本笔记本的金额比较结果是, 即

       ,已知,,在直角坐标系中画图,可知直线的斜率始终为负, 故有, 所以选B

    8.由已知得小圆半径, 三点组成正三角形, 边长为球的半径, 所以有

    , , 所以球的表面积.

    9.设, 则在椭圆中, 有,  ,  而在双曲线中, 有

        , ,  ∴

    10. 解：5个有效分为84，84，86，84，87；其平均数为85。利用方差公式可得方差为1.6．

    二．填空题：11、；  12、；  13、；  14、；15、；

    解析：

    11.解：设向量与的夹角为且∴，则=.

    12. 设, 则有,

     根据小车的转动情况,  可大胆猜测只有时, .

    13. 设正方体的棱长为, 过点作直线交的延长线于, 连, 在中, , , , ∴

    14. 解：把直线代入得

    ，弦长为

    15.解：连接，PC是⊙O的切线，∴∠OCP=Rt∠．

    ∵30°，OC==3， ∴，即PC=．

    三．解答题：

    16.解: （I） 共有种结果　　　　　　………………4分　

    （II） 若用(a,b)来表示两枚骰子向上的点数，则点数之和是3的倍数的结果有：

    （1,2），（2,1），（1,5），（5,1），（2,4），（4,2），

    （3,3），（4,5），（5,4），（3,6），（6,3），（6,6）

    共12种．                                     　 ………………8分

    　（III）两枚骰子点数之和是3的倍数的概率是：P＝ 　　   …………12分

     

    17．（１）若，则， ∵函数是定义在上的偶函数，

    ∴     ----------3分

    （２）当时，．   --------------6分

    显然当时,;当时,，又在和处连续，

    ∴函数在上为减函数，在上为增函数.   -----------8分

    （3）∵函数在上为增函数，且，

    ∴当时，有，------------------10分

    又当时，得且， 即

    ∴   即得.    ----------12分

     

    18．（１）由已知,  得平面, 

    又,   ∴平面, 

    ∴为二面角的平面角.    ----------3分

    由已知,  得,

    ∵是斜边 上的中线, 

    ∴为等腰三角形,  ,

    即二面角的大小为.    -------------7分

    （２）显然.  若, 则平面, 

    而平面，故平面与平面重合，与题意不符.

    由是，则必有，

    连BD，设，由已知得，从而，

    又，∴，得，

    故平面，                      -----------10分

    ∴，又，∴平面,  ∴，反之亦然.

    ∵   ∴ ,  ∴∽  -------12分

    ∴.    --------14分

     

    19．（１）由题意得，

       -----------3分

    又， ∴数列是首项为、公比为的等比数列，-----------6分

    ∴   --------------7分

    （2）∵,

      ∴，     ---------12分

    ∴当时，   ------------14分

    20．以为原点，湖岸线为轴建立直角坐标系，  设OA的倾斜角为，点P的坐标为,

        ，则有　               ………………3分

                  -------------7分

        由此得 -------------9分

    即 -------------12分

    故营救区域为直线与圆围城的弓形区域.(图略)--------14分

    21．（１）由题意知，   可得．--------2分

    ∵， ∴，  有 ．  --------4分

    （２）以为原点，所在直线为轴建立直角坐标系，

    设，点的坐标为，                    -------5分

    ∵ ，  ∴， ．  -------6分

    ∴,  ∴． ------8分

    设，则当时，有．

    ∴在上增函数，∴当时，取得最小值，

    从而取得最小，此时 ．    ---------------------11分

    设椭圆方程为，

    则，解之得，故 ．--------14分


    同步练习册答案