
题目列表(包括答案和解析)
A.(a*b)*a=a B.[a*(b*a)]*(a*b)=a
C.b*(b*b)=b D.(a*b)* [b*(a*b)]=b
函数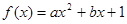 (
(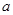 、
、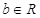 )满足:
)满足: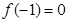 ,且对任意实数x均有
,且对任意实数x均有
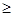 0成立
0成立
(1)求实数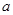 、
、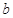 的值;
的值;
(2)当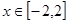 时,求函数
时,求函数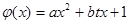 的最大值
的最大值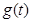 .
.
【解析】(1) 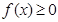 恒成立
恒成立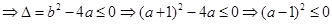 .
.
(2) 
对称轴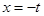 ,由于开口方向向上,所以求最大值时对称轴要与区间中间进行比较讨论即可.
,由于开口方向向上,所以求最大值时对称轴要与区间中间进行比较讨论即可.
如果函数 的定义域为
的定义域为 ,对于
,对于 ,恒有
,恒有 ,且
,且 是不大于5 的正整数,当
是不大于5 的正整数,当 时,
时, .那么具有这种性质的函数
.那么具有这种性质的函数 = .(注:填上你认为正确的一个函数即可)
= .(注:填上你认为正确的一个函数即可)
(15分)已知 是数列
是数列 的前
的前 项和,
项和, (
( ,
, ),且
),且 .
.
(1)求 的值,并写出
的值,并写出 和
和 的关系式;
的关系式;
(2)求数列 的通项公式及
的通项公式及 的表达式;
的表达式;
(3)我们可以证明:若数列 有上界(即存在常数
有上界(即存在常数 ,使得
,使得 对一切
对一切 恒成立)且单调递增;或数列
恒成立)且单调递增;或数列 有下界(即存在常数
有下界(即存在常数 ,使得
,使得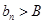 对一切
对一切 恒成立)且单调递减,则
恒成立)且单调递减,则 存在.直接利用上述结论,证明:
存在.直接利用上述结论,证明: 存在.
存在.
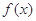 的定义域为
的定义域为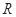 ,对于
,对于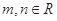 ,恒有
,恒有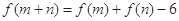 ,且
,且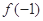 是不大于5 的正整数,当
是不大于5 的正整数,当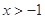 时,
时,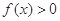 .那么具有这种性质的函数
.那么具有这种性质的函数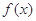 = .(注:填上你认为正确的一个函数即可)
= .(注:填上你认为正确的一个函数即可) 湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com