题目列表(包括答案和解析)
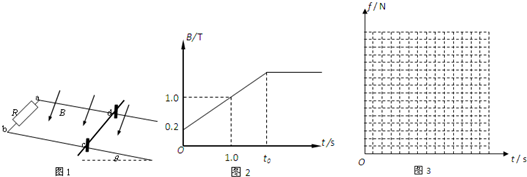
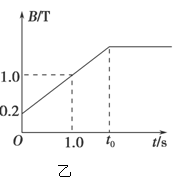
两根平行金属导轨固定倾斜放置，与水平面夹角为37°，相距d＝0.5 m，a、b间接一个电阻为R＝1.5 Ω.在导轨上c、d两点处放一根质量m＝0.05 kg的金属棒，bc长L＝1 m，金属棒与导轨间的动摩擦因数μ＝0.5.金属棒与导轨接触点间电阻r＝0.5 Ω， 金属棒被两个垂直于导轨的木桩顶住而不会下滑，如图甲所示．在金属导轨区域加一个垂直导轨斜向下的匀强磁场，磁场随时间的变化关系如图乙所示．重力加速度g＝10 m/s2.(sin 37°＝0.6，cos 37°＝0.8)．求：
(1)0～1.0 s内回路中产生的感应电动势大小；
(2)t＝0时刻，金属棒所受的安培力大小；
(3)在磁场变化的全过程中，若金属棒始终没有离开木桩而上升，则图乙中t0的最大值；
(4)通过计算在图中画出0～t0max内金属棒受到的静摩擦力随时间的变化图象．
 | |||
 | |||
两根足够长的固定平行金属光滑导轨位于同一水平面，导轨上横放着两根相同的导体棒ab、cd与导轨构成矩形回路。导体棒的两端连接着处于压缩状态的两根轻质弹簧，两棒的中间用细线绑住，它们的电阻均为R，回路上其余部分的电阻不计。在导轨平面内两导轨间有一竖直向下的匀强磁场。开始时，导体棒处于静止状态，剪断细线后，导体棒运动过程中（ ）
| A．回路中有感应电动势 |
| B．两根导体棒所受安培力的方向相同 |
| C．两根导体棒和弹簧构成的系统机械能守恒 |
| D．两根导体棒和弹簧构成的系统机械能不守恒 |
（10分）两根平行金属导轨固定倾斜放置，与水平面夹角为37°，相距d＝0.5 m，a、b间接一个电阻为R＝1.5 Ω.在导轨上c、d两点处放一根质量m＝0.05 kg的金属棒，bc长L＝1 m，金属棒与导轨间的动摩擦因数μ＝0.5.金属棒与导轨接触点间电阻r＝0.5 Ω， 金属棒被两个垂直于导轨的木桩顶住而不会下滑，如图甲所示．在金属导轨区域加一个垂直导轨斜向下的匀强磁场，磁场随时间的变化关系如图乙所示．重力加速度g＝10 m/s2.(sin 37°＝0.6，cos 37°＝0.8)．求：
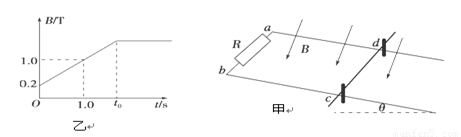
(1)0～1.0 s内回路中产生的感应电动势大小；
(2)t＝0时刻，金属棒所受的安培力大小；
(3)在磁场变化的全过程中，若金属棒始终没有离开木桩而上升，则图乙中t0的最大值；
(4)通过计算在图中画出0～t0max内金属棒受到的静摩擦力随时间的变化图象．
两根足够长的固定平行金属光滑导轨位于同一水平面，导轨上横放着两根相同的导体棒ab、cd与导轨构成矩形回路。导体棒的两端连接着处于压缩状态的两根轻质弹簧，两棒的中间用细线绑住，它们的电阻均为R，回路上其余部分的电阻不计。在导轨平面内两导轨间有一竖直向下的匀强磁场。开始时，导体棒处于静止状态，剪断细线后，导体棒运动过程中（ ）
A．回路中有感应电动势
B．两根导体棒所受安培力的方向相同
C．两根导体棒和弹簧构成的系统机械能守恒
D．两根导体棒和弹簧构成的系统机械能不守恒
一、选择题（每题4分共40分）
1、B 2、D 3、B 4、ABD 5、B 6、ABD 7、C 8、ACD 9、AD 10、DC
二、实验题（两题共14分）
|
， 
……………①（4分）
…………②（4分）
…………③（2分）
= 0.2
（1分）
－
（2分）
，设木块离开地面间速度为V
③ （1分）
④
（3分）
⑤
（3分）
由④⑤式可得 T=4N （1分）
（2分）
(1分)，
(1分)
（2分）
（１分）
（1分）
得
（2分）