练习册

  • 练习册
  • 试题
    一质量为M=2.0kg的小物块随足够长的水平传送带一起匀速向右运动.被一水平向左飞来的子弹击中.且子弹从物块中穿过.子弹和物块的作用时间极短.如图(11)所示．地面观察者记录的小物块被击中后的速度随时间变化关系如图(11)乙所示(图中取向右运动的方向为正方向)．已知传送带的速度保持不变.g取10m/s2．求:(1)传送带的速度υ的大小,(2)物块与传送带的动摩擦因数μ,(3)传送带对物块所做的功． 【查看更多】

     

    题目列表(包括答案和解析)

    一质量为m=2.0kg的小物块随足够长的水平传送带一起运动，被一水平向左飞来的子弹击中并从物块中穿过，如图1所示．固定在传送带右端的位移传感器纪录了小物块被击中后的位移随时间的变化关系如图2所示（图象前3s内为二次函数，3-4.5s内为一次函数，取向左运动的方向为正方向）．已知传送带的速度保持不变，g取10m/s2．），则下列说法错误的是（　　）

    查看答案和解析>>

    一质量为m=2.0kg的小物块随足够长的水平传送带一起运动，被一水平向左飞来的子弹击中并从物块中穿过，如图1所示．固定在传送带右端的位移传感器纪录了小物块被击中后的位移随时间的变化关系如图2所示（图象前3s内为二次函数，3-4.5s内为一次函数，取向左运动的方向为正方向）．已知传送带的速度保持不变，g取10m/s2，求：
    （1）定性描述小物块在前3s内的运动情况
    （2）传送带速度v的大小和方向
    （3）物块与传送带间的动摩擦因数μ

    查看答案和解析>>

    一质量为M=2.0kg的小物块随足够长的水平传送带一起向右匀速运动，被一水平向左飞来的子弹击中，且子弹从小物块中穿过，子弹和小物块的作用时间极短，如图甲所示．地面观察者记录的小物块被击中后的速度随时间变化关系如图乙所示（图中取向右运动的方向为正方向）．已知传送带的速度保持不变，g取10m/s2．求：
    （1）传送带的速度v的大小；
    （2）小物块与传送带之间的动摩擦因数μ；
    （3）传送带对小物块所做的功．

    查看答案和解析>>

    一质量为m=2.0kg的小物块随足够长的水平传送带一起运动，被一水平向左飞来的子弹击中并从物块中穿过，如图1所示．固定在传送带右端的位移传感器纪录了小物块被击中后的位移随时间的变化关系如图2所示（图象前3s内为二次函数，3-4.5s内为一次函数，取向左运动的方向为正方向）．已知传送带的速度保持不变，g取10m/s2．
    （1）指出传送带速度v的方向及大小，说明理由；
    （2）求物块与传送带间的动摩擦因数μ
    精英家教网

    查看答案和解析>>

    一质量为m=2.0kg的小物块随足够长的水平传送带一起运动，被一水平向左飞来的子弹击中并从物块中穿过，如图1所示．固定在传送带右端的位移传感器纪录了小物块被击中后的位移随时间的变化关系如图2所示（图象前3s内为二次函数，3-4.5s内为一次函数，取向左运动的方向为正方向）．已知传送带的速度保持不变，g取10m/s2．
    精英家教网
    （1）定性描述小物块在前3s内的运动情况；
    （2）求传送带速度v的大小；
    （3）求物块与传送带间的动摩擦因数μ．

    查看答案和解析>>

    一、选择题（每题4分共40分）

    1、B  2、D  3、B  4、ABD  5、B  6、ABD   7、C   8、ACD    9、AD   10、DC

    二、实验题（两题共14分）

    R

     

    12、（4分）

     

     

     

     

     

     

     

    （4分）   

    三、计算题（四题共46分）

    13.解：设篮球从篮板处飞到甲处所用时间为t1，从甲处飞到乙处所用时间为t2,则

     ，      ……………①（4分）

    篮球从甲处飞到乙处过程中，有

          …………②（4分）

    联立①②解得：       …………③（2分）

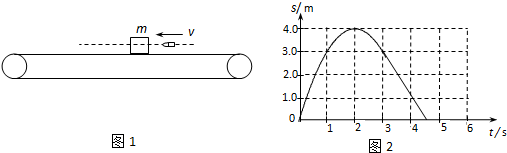
    14、解：（1）传送带的速度υ的大小为2.0 m/s，方向向右．            （2分）

    （2）由速度图象可得，物块在滑动摩擦力的作用下

    做匀变速运动的加速度为  a=ㄓυ/ㄓt=2.0 m/s2                     （1分）

    由牛顿第二定律得            f = μMg= Ma                     （2分）

    得到物块与传送带间的动摩擦因数 μ == 0.2                   （1分）

    （3）从子弹离开物块到物块与传送带一起匀速运动的过程中，设传送带对物块所做的功为W，由动能定理得：W =ㄓEk = －           （2分）

    从速度图象可知：   υ1=4.0 m/s    υ2 = υ = 2.0 m/s             （1分）

    解得：   W= －12J                                        （1分）

    15、解：（1）子弹打木块过程、满足动量守恒，碰后二者的共同速度为V1

                mVo=(M+m)V1   ①        （2分）         

    在拉紧瞬间木块失去了沿绳方向的速度，此时绳子与水平面夹角为，设木块离开地面间速度为V

               V=V1sin        ②      （1分）

               sin=          ③     （1分）

    由①②③式得V=10m/s    （1分）                            

    （2）木块离地以后的运动满足机械能守恒则

                     ④   （3分）

              T+(M+m)g=(M+m)                                                  ⑤   （3分）

    由④⑤式可得 T=4N     （1分）                          

     

     

    16、解：（1）由动能定理得  （2分）

    解得v0=1.0×104m/s （1分）

    （2）微粒在偏转电场中做类平抛运动L=v0t,(1分)(1分)，(1分)

    飞出电场时，速度偏转角的正切为 （2分）

    解得  U2=100V （1分）

    （3）进入磁场时微粒的速度是    （１分）

    轨迹如图，由几何关系得，轨道半径   （1分）

    由洛伦兹力充当向心力：得 （2分）

    解得B＝0.20T （1分）

    所以，为使微粒不会由磁场右边射出，该匀强磁场的磁感应强度B至少为0.20T

     

     

     

     

     

     

     

     

     

     

     

     

     

     

     

     

     

     

     

     

     


    同步练习册答案