
题目列表(包括答案和解析)
同学4人各写一张贺卡,先集中起来,然后每人从中任取一张贺卡;求下列条件的概率:
(1) 每人拿到的1张贺卡都是自己写的概率;
(2) 有且只有1个人拿到的贺卡是自己写的概率
【解析】本试题主要考查了古典概型的运用。解决该试题的关键是理解一次试验的所有基本事件数,然后结合事件A发生的事件数,利用比值可以得到概率值。
(理科做)已知![]()
(I) 若a=3,求![]() 的单调区间和极值;
的单调区间和极值;
(II)已知![]() 是
是![]() 的两个不同
的两个不同![]() 的极值点,且
的极值点,且![]() ,若
,若![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围。
的取值范围。
(理)给 个自上而下相连的正方形着黑色或白色。当
个自上而下相连的正方形着黑色或白色。当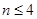 时,在所有不同的着色方案中,黑色正方形互不相邻的着色方案如下图所示
时,在所有不同的着色方案中,黑色正方形互不相邻的着色方案如下图所示

由此推断,当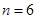 时,黑色正方形互不相邻的着色方案共有 种,至少有两个黑色正方形相邻的着色方案共有 种,(结果用数值表示)
时,黑色正方形互不相邻的着色方案共有 种,至少有两个黑色正方形相邻的着色方案共有 种,(结果用数值表示)
(理科)把一组邻边分别为1和 的矩形ABCD沿对角线AC折成直二面角B—AC—D且使A、B、C、D四点在同一球面上,则该球的体积为
▲
的矩形ABCD沿对角线AC折成直二面角B—AC—D且使A、B、C、D四点在同一球面上,则该球的体积为
▲
(文科)正四面体V—ABC的棱长为2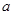 ,E,F,G,H分别是VA,VB,BC,AC的
,E,F,G,H分别是VA,VB,BC,AC的
中点,则四边形EFGH面积是___________▲____ 。
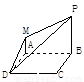
(理科做)已知
(I) 若a=3,求 的单调区间和极值;
的单调区间和极值;
(II)已知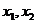 是
是 的两个不同的极值点,且
的两个不同的极值点,且 ,若
,若 恒成立,求实数
恒成立,求实数 的取值范围。
的取值范围。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com