题目列表(包括答案和解析)
（本小题满分15分）
已知函数
，其中
，
（
），若
相邻两对称轴间的距离不小于
．
（Ⅰ）求
的取值范围；
（Ⅱ）在
中，
分别是角
的对边，
，当最大时，
，求的面积．
（本小题满分15分）
某旅游商品生产企业，2009年某商品生产的投入成本为1元/件，
出厂价为流程图的输出结果
元/件，年销售量为10000件，
因2010年国家长假的调整，此企业为适应市场需求，
计划提高产品档次，适度增加投入成本．若每件投入成本增加的
比例为
（
），则出厂价相应提高的比例为
，
同时预计销售量增加的比例为
．
已知得利润
（出厂价
投入成本）
年销售量．
（Ⅰ）写出2010年预计的年利润
与投入成本增加的比例的关系式；
（Ⅱ）为使2010年的年利润比2009年有所增加，
问：投入成本增加的比例应在什么范围内？
（本小题满分15分）某地有三个村庄，分别位于等腰直角三角形ABC的三个顶点处，已知AB=AC=6km，现计划在BC边的高AO上一点P处建造一个变电站. 记P到三个村庄的距离之和为y.
（1）设
，把y表示成
的函数关系式；
（2）变电站建于何处时，它到三个小区的距离之和最小？
（本小题满分15分）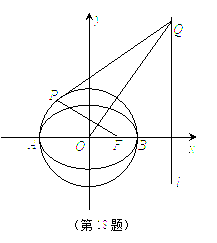
如图，已知圆O：x2+y2=2交x轴于A，B两点，曲线C是以AB为长轴，离心率为
的椭圆，其右焦点为F．若点P(－1,1)为圆O上一点，连结PF，过原点O作直线PF的垂线交椭圆C的右准线l于点Q．（1）求椭圆C的标准方程；
（2）证明：直线PQ与圆O相切．
（本小题满分15分）已知等差数列{an}中，首项a1＝1，公差d为整数，且满足a1+3＜a3，a2+5＞a4，数列{bn}满足
，其前n项和为Sn．（1）求数列{an}的通项公式an；（2）若S2为S1，Sm(m∈N*)的等比中项，求正整数m的值．
一、填空题：
1．
； 2．
； 3．
； 4．
； 5．
；
6．
； 7．
8．
； 9．21； 10．
；
11．
；12．
； 13．
； 14．
二、解答题：
15．（1）编号为016； ----------------------------3分
（2）
分组
频数
频率
60.5~70.5
8
0.16
70.5~80.5
10
0.20
80.5~90.5
18
0.36
90.5~100.5
14
0.28
合计
50
1
------------- ----------------------------8分
（3）在被抽到的学生中获二奖的人数是9+7=16人，
占样本的比例是
，即获二等奖的概率约为32%，
所以获二等奖的人数估计为800×32%=256人。有 ------------------------13分
答：获二等奖的大约有256人。 -----------------------------------14分
16．解：（1） B=600，A＋C＝1200， C＝1200 －A，
∴ sinA－sinC＋
cos（A－C）
＝
sinA－
cosA＋［1－2sin2（A－60°）］=，
∴sin（A－60°）［1－
sin（A－60°）］＝0?
-------------------------4分
∴sin（A－60°）＝0或sin（A－60°）＝， 又0°＜A＜120°，
∴A＝60°或105°．??? -------------------------8分
(2) 当A＝60°时，Ｓ△＝ａcsinB＝×4Ｒ2sin360°＝
------------11分
当A＝105°时,?S△＝×4Ｒ2?sin105°sin15°sin60°＝
----------------14分
17．解：（1）如四面体A1-ABC或四面体C1-ABC或四面体A1-ACD或四面体C1-ACD； ---4分
（2）如四面体B1-ABC或四面体D1-ACD； -------------------------8分
（3）如四面体A-B1CD1（3分 ）； -------------------------11分
设长方体的长、宽、高分别为
，则
．---------14分
18．（1）如图，由光学几何知识可知，点
关于
的对称点
在过点
且倾斜角为
的直线
上。在
中，椭圆长轴长
， ----4分
又椭圆的半焦距
，∴
，
∴所求椭圆的方程为
．
-----------------------------7分
（2）路程最短即为上上的点
到圆
的切线长最短，由几何知识可知，应为过原点且与垂直的直线与的交点，这一点又与点
关于对称，∴
，故点的坐标为
．
-------------------------15分
注：用代数方法求解同样分步给分！
19． 解：（1）若
，对于正数
，
的定义域为
，但 的值域
，故
，不合要求． --------------------------2分
若
，对于正数，的定义域为
． -----------------3分
由于此时
，
故函数的值域
．
------------------------------------6分
由题意，有
，由于
，所以
．------------------8分
20．解：（1）依题意数列
的通项公式是
，
故等式即为
，
同时有
，
两式相减可得
------------------------------3分
可得数列
的通项公式是
，
知数列是首项为1，公比为2的等比数列。 ---------------------------4分
（2）设等比数列的首项为，公比为
，则
，从而有：
，
又
，
故
-----------------------------6分
，
要使
是与
无关的常数，必需
， ----------------------------8分
即①当等比数列的公比时，数列是等差数列，其通项公式是
；
②当等比数列的公比不是2时，数列不是等差数列． ------------9分
（3）由（2）知
， ------------------------------------------10分
--------------14分
----------------------------16分
|
是
的中点，
；
---------------------------------------------------------4分
的特征多项式为
，
, -----------------------------------------------------------------------5分
,当
．
----------------------------------------6分
，得
． -------------------------------------7分
．--------------------10分
，∴
， 
，
，三个同向正值不等式相乘得
．------------------------------5分
时原不等式仍然成立．
、
、
、
证；
．-------------------------------------10分
，则
码---------------------------------------------------------------2分
----------------------------------------------4分
的可能取值为2，3，4，5，--------------------------------------5分
，
，
+
． --------------------------------------------------8分
． --------------------------------9分
；所求数学期望是
．----------------------------10分