
题目列表(包括答案和解析)
(13分,理科做)已知函数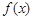 的定义域为
的定义域为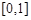 ,且同时满足:①
,且同时满足:①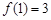 ;②
;②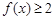 恒成立;③若
恒成立;③若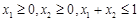 ,则有
,则有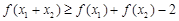 .
.
(1)试求函数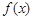 的最大值和最小值;
的最大值和最小值;
(2)试比较 与
与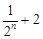 的大小
的大小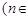 N);
N);
(3)某人发现:当x= (nÎN)时,有f(x)<2x+2.由此他提出猜想:对一切xÎ(0,1
(nÎN)时,有f(x)<2x+2.由此他提出猜想:对一切xÎ(0,1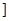 ,都有
,都有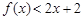 ,请你判断此猜想是否正确,并说明理由.
,请你判断此猜想是否正确,并说明理由.
(1)试求函数f(x)的最大值和最小值;
(2)试比较f(![]() n)与
n)与![]() n+2的大小(n∈N);
n+2的大小(n∈N);
(3)某人发现:当x=![]() n(n∈N)时,有f(x)<2x+2.由此他提出猜想:对一切x∈(0,1],都有f(x)<2x+2,请你判断此猜想是否正确,并说明理由.
n(n∈N)时,有f(x)<2x+2.由此他提出猜想:对一切x∈(0,1],都有f(x)<2x+2,请你判断此猜想是否正确,并说明理由.
| A、是等比数列 | B、是等差数列 | C、从第2项起是等比数列 | D、是常数列 |
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com