
题目列表(包括答案和解析)
在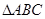 中,角
中,角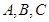 的对边分别为
的对边分别为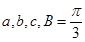 ,
, 。
。
(1)求 的值;
的值;
(2)求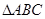 的面积.
的面积.
【解析】本试题主要是考查了解三角形中正弦定理和三角形面积公式的运用。
在△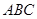 中,
中,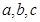 分别为内角
分别为内角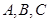 的对边,且
的对边,且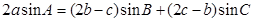 .
.
(1)求角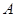 的大小;
的大小;
(2)若 +
+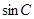 =
=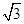 ,试判断△
,试判断△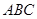 的形状.
的形状.
【解析】本试题主要考查了解三角形中正弦定理和余弦定理的运用。求解变和角,并定形的问题。
在△ 中,
中, 分别为内角
分别为内角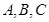 的对边,且
的对边,且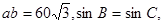 △
△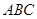 的面积为15
的面积为15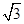 ,求边
,求边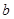 的长.
的长.
【解析】本试题主要考查了解三角形的运用,求解三角形的边长和面积的运算。
在△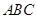 中,∠
中,∠ ,∠
,∠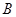 ,∠
,∠ 的对边分别是
的对边分别是 ,且
,且
 .
.
(1)求∠ 的大小;(2)若
的大小;(2)若 ,
, ,求
,求 和
和 的值.
的值.
【解析】第一问利用余弦定理得到
 第二问
第二问
(2) 由条件可得 
将  代入 得 bc=2
代入 得 bc=2
解得 b=1,c=2 或 b=2,c=1 .
在 中,已知
中,已知
 ,面积
,面积 ,
,
(1)求 的三边的长;
的三边的长;
(2)设 是
是 (含边界)内的一点,
(含边界)内的一点, 到三边
到三边 的距离分别是
的距离分别是
①写出 所满足的等量关系;
所满足的等量关系;
②利用线性规划相关知识求出 的取值范围.
的取值范围.
【解析】第一问中利用设 中角
中角 所对边分别为
所对边分别为
由 得
得
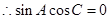

又由 得
得 即
即

又由 得
得 即
即

又
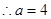 又
又 得
得
即 的三边长
的三边长

第二问中,① 得
得

故
②
令 依题意有
依题意有
作图,然后结合区域得到最值。

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com