
题目列表(包括答案和解析)
(本小题满分13分)
由于当前学生课业负担较重,造成青少年视力普遍下降,现从某中学随机抽取16名学生,经校医用对数视力表检査得到每个学生的视力状况的茎叶图(以小数点前的一位数字为茎,小数点后的一位数字为叶)如右:

(Ⅰ)若视力测试结果不低于5.0,则称为“好视力”,求校医从这16人中随机选取3人,至多有1人是“好视力”的概率;
(Ⅱ)以这16人的样本数据来估计整个学校的总体数据,若从该校(人数很多)任选3人,记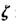 表示抽到“好视力”学生的人数,求
表示抽到“好视力”学生的人数,求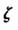 的分布列及数学期望.
的分布列及数学期望.
(本小题满分13分)
为拉动经济增长,某市决定新建一批重点工程,分别为基础设施工程、民生工程和产业建设工程三类.这三类工程所含项目的个数分别占总数的![]() ,
,![]() ,
,![]() .现在3名工人独立地从中任选一个项目参与建设。
.现在3名工人独立地从中任选一个项目参与建设。
(I)求他们选择的项目所属类别互不相同的概率;
(II)记![]() 为3人中选择的项目属于基础设施工程或产业建设工程的人数,求
为3人中选择的项目属于基础设施工程或产业建设工程的人数,求![]() 的分布列及数学期望。
的分布列及数学期望。
(本小题满分13分)
为拉动经济增长,某市决定新建一批重点工程,分别为基础设施工程、民生工程和产业建设工程三类.这三类工程所含项目的个数分别占总数的![]() ,
,![]() ,
,![]() .现在3名工人独立地从中任选一个项目参与建设。
.现在3名工人独立地从中任选一个项目参与建设。
(I)求他们选择的项目所属类别互不相同的概率;
(II)记![]() 为3人中选择的项目属于基础设施工程或产业建设工程的人数,求
为3人中选择的项目属于基础设施工程或产业建设工程的人数,求![]() 的分布列及数学期望。
的分布列及数学期望。
(本小题满分13分)
椭圆 :
: 与抛物线
与抛物线 :
: 的一个交点为M,抛物线
的一个交点为M,抛物线 在点M处的切线过椭圆
在点M处的切线过椭圆 的右焦点F.
的右焦点F.

(Ⅰ)若M ,求
,求 和
和 的标准方程;
的标准方程;
(II)求椭圆 离心率的取值范围.
离心率的取值范围.
(本小题满分13分)
已知圆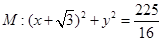 的圆心为
的圆心为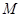 ,圆
,圆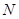 :
: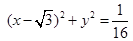 的圆心为
的圆心为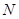 ,一动圆与圆
,一动圆与圆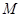 内切,与圆
内切,与圆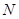 外切.
外切.
(Ⅰ)求动圆圆心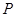 的轨迹方程;
的轨迹方程;
(Ⅱ)在(Ⅰ)所求轨迹上是否存在一点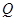 ,使得
,使得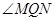 为钝角?若存在,求出点
为钝角?若存在,求出点 横坐标的取值范围;若不存在,说明理由.
横坐标的取值范围;若不存在,说明理由.
命题人:黄小红(株洲县五中) 赵家早(株洲县五中) 郭珂珊(潇湘双语)
审题人:郭珂珊 (潇湘双语) 赵家早(株洲县五中) 黄小红(株洲县五中)
第Ⅰ卷(选择题)
一.选择题:本大题共10小题,每小题5分,共50分,在每小题给出的四个选项中,只有一项是符合要求的.答案要写在答题卷上。
题号
1
2
3
4
5
6
7
8
9
10
答案
D
A
D
D
C
A
C
B
C
C
第Ⅱ卷(非选择题)
二、填空题:本大题共5小题,每小题5分 ,共25分,把答案填在答题卡中对应题号后的横线上.
11. -160
12. 数学理科.files/image250.gif) 13.
13.
数学理科.files/image252.gif)
14.-数学理科.files/image254.gif) ; 15. (1)617 (2)4040
; 15. (1)617 (2)4040
三.解答题:本大题共6小题,共75分。解答应写出文字说明,证明过程或演算步骤。
16.解(Ⅰ)数学理科.files/image256.gif) ,……2分
,……2分
由数学理科.files/image258.gif) 得
得数学理科.files/image260.gif) ,……… 3分
,……… 3分
所以数学理科.files/image262.gif) ,( 4分)
,( 4分)
所以数学理科.files/image264.gif) ………6分
………6分
(Ⅱ)由f(B)=数学理科.files/image266.gif) 1得
1得数学理科.files/image268.gif) ,解得
,解得数学理科.files/image270.gif) ………8分
………8分
又由数学理科.files/image175.gif) 知
知数学理科.files/image272.gif) ,所以
,所以数学理科.files/image274.gif) ………10分
………10分
由余弦定理知
数学理科.files/image276.gif) =
=数学理科.files/image278.gif)
所以数学理科.files/image280.gif) ……… 12分
……… 12分
17.解:记“第一关第一次过关”为事件A1,“第一关第二次过关”为事件A2;记“第二关第一次过关”为事件B1,“第二关第二次过关”为事件B2;………1分
(Ⅰ)王同学获得1000元奖金的概率为:
则数学理科.files/image282.gif) ………5分
………5分
(Ⅱ)王同学获得奖金额数学理科.files/image183.gif) 可能取值为:0 元,1000 元, 4000 元
………6分
可能取值为:0 元,1000 元, 4000 元
………6分
数学理科.files/image284.gif) (7分)
(7分) 数学理科.files/image286.gif) ………8分
………8分
数学理科.files/image288.gif)
数学理科.files/image290.gif) …………10分
…………10分
(另解:数学理科.files/image292.gif) =1-
=1-数学理科.files/image294.gif) -
-数学理科.files/image296.gif) =
=数学理科.files/image298.gif) …………10分)
…………10分)
数学理科.files/image300.gif) ……… 12分
……… 12分
18. (本小题满分12分)
解(Ⅰ)证明:取数学理科.files/image302.gif) 中点
中点数学理科.files/image304.gif) ,连接
,连接数学理科.files/image306.gif) ,
,数学理科.files/image308.gif) ,
又G为AD中点
,
又G为AD中点
数学理科.files/image310.gif) , GH
, GH数学理科.files/image312.gif)
数学理科.files/image314.gif) , ………分
, ………分
同理可证 数学理科.files/image316.gif) ,
,
数学理科.files/image318.gif) ………3分
………3分
数学理科.files/image320.gif) ,
, 数学理科.files/image322.gif)
数学理科.files/image324.gif) ……… 4分
……… 4分
(Ⅱ)延长CE,过D作DO垂直直线EC于O,易证DO⊥平面ABCE,AE⊥EC,AE⊥DE,二面角D-AE-C的平面角大小为数学理科.files/image326.gif) .
.
∴数学理科.files/image328.gif)
∵DE=数学理科.files/image330.gif) ,∴OE=1,DO=2
,∴OE=1,DO=2
以数学理科.files/image332.gif) 为原点,
为原点,数学理科.files/image334.gif) 为y轴正方向建立坐标系O-xyz
(图略)
为y轴正方向建立坐标系O-xyz
(图略)
则D(0,0,2),A(2,1,0),E(0,1,0) ,C(0,2,0),B(2,2,0),
H(2,数学理科.files/image336.gif) ,0),G(1,
,0),G(1,数学理科.files/image066.gif) ,1),F(0,
,1),F(0,数学理科.files/image336.gif) ,0)………6分
,0)………6分
数学理科.files/image339.gif) ,
,数学理科.files/image341.gif)
数学理科.files/image343.gif)
数学理科.files/image345.jpg) ∴异面直线GF与BD所成的角为
∴异面直线GF与BD所成的角为数学理科.files/image347.gif) ………8分
………8分
(Ⅲ)取DC中点P,易证OP⊥平面BCD,所以面BCD一个法向量为数学理科.files/image349.gif) …
9分
…
9分
数学理科.files/image351.gif) (0,1,0),
(0,1,0), 数学理科.files/image353.gif) (-2,-2,2),设平面
(-2,-2,2),设平面数学理科.files/image355.gif) 的法向量为
的法向量为数学理科.files/image357.gif)
数学理科.files/image359.gif) ,
,
取x=1,得y=0,z=1,得平面数学理科.files/image355.gif) 的一个法向量为
的一个法向量为数学理科.files/image361.gif) ………
10分
………
10分
∴数学理科.files/image363.gif) ……… 11分
……… 11分
∴二面角A-BD-C的大小为120°。……… 12分
19.(本小题满分13分)
解:(Ⅰ)第1年贷款(32000+5000)万元,第2年5000×数学理科.files/image365.gif) 万元…,第n年贷款5000×
万元…,第n年贷款5000×数学理科.files/image367.gif) 万元 …1分
万元 …1分
所以贷款总额为:数学理科.files/image221.gif) =32000+5000+5000×
=32000+5000+5000×数学理科.files/image365.gif) +…+5000×
+…+5000×数学理科.files/image367.gif) =52000-20000
=52000-20000数学理科.files/image369.gif) … 3分
… 3分
同理:第1年利润4000万元,第2年利润4000×(1+数学理科.files/image218.gif) )万元,…,
)万元,…,
第n年利润4000×数学理科.files/image372.gif) 万元 …………4分
万元 …………4分
数学理科.files/image223.gif) =4000+4000×
=4000+4000×数学理科.files/image374.gif) +……+4000×
+……+4000×数学理科.files/image372.gif) =12000[
=12000[数学理科.files/image377.gif) -1]
………… 6分
-1]
………… 6分
(Ⅱ) 由题意数学理科.files/image379.gif) >0, (7分) 12000[
>0, (7分) 12000[数学理科.files/image377.gif) -1]>52000-20000
-1]>52000-20000数学理科.files/image369.gif) ……8分
……8分
化简得,3×数学理科.files/image377.gif) +5×
+5×数学理科.files/image369.gif) -16>0?
…………9分
-16>0?
…………9分
设x=数学理科.files/image381.gif) ,3x2-16x+5>0?∴x<
,3x2-16x+5>0?∴x<数学理科.files/image218.gif) (舍)或x>5 …………10分
(舍)或x>5 …………10分
?∴数学理科.files/image377.gif) >5, 而
>5, 而数学理科.files/image384.gif) ……………11分
……………11分
∴n≥6. (12分) ∴经过6年公司总利润才能超过无息贷款总额 ………13分
20.(本小题满分13分)
解.(Ⅰ) 数学理科.files/image386.gif)
数学理科.files/image388.gif) ), 则
), 则 数学理科.files/image390.gif) ………1分
………1分
因为数学理科.files/image392.gif) , 所以当
, 所以当数学理科.files/image394.gif) 时,
时,数学理科.files/image396.gif) 对
对数学理科.files/image398.gif) 恒成立,
恒成立,
故F(x)在(0,3)内单调递减,(2分 ),
而F(x)在x=3处连续 , 所以数学理科.files/image400.gif) ………3分
………3分
当数学理科.files/image402.gif) 时,
时,数学理科.files/image404.gif) 时
时数学理科.files/image406.gif) ,
,数学理科.files/image408.gif) 时
时数学理科.files/image410.gif) ,所以F(x)在
,所以F(x)在数学理科.files/image412.gif) 内单调递减,在
内单调递减,在数学理科.files/image414.gif) 内单调递增。………4分
内单调递增。………4分
所以数学理科.files/image416.gif) ………5分
………5分
综上所述,当数学理科.files/image394.gif) 时,
时,数学理科.files/image418.gif) ,当
,当数学理科.files/image402.gif) 时,
时,数学理科.files/image420.gif) 。………6分
。………6分
(Ⅱ)若数学理科.files/image422.gif) 的图象与
的图象与数学理科.files/image424.gif) 的图象恰有四个不同交点, 即
的图象恰有四个不同交点, 即数学理科.files/image426.gif) 有四个不同的根, ………7分
有四个不同的根, ………7分
亦即 数学理科.files/image428.gif) 有四个不同的根。 ………8分
有四个不同的根。 ………8分
令数学理科.files/image430.gif) ,
,
则数学理科.files/image432.gif) 。………………………9分
。………………………9分
当数学理科.files/image434.gif) 变化时
变化时数学理科.files/image436.gif) 的变化情况如下表:
的变化情况如下表:
数学理科.files/image434.gif)
数学理科.files/image439.gif)
(-1,0)
(0,1)
(1,数学理科.files/image441.gif) )
)
数学理科.files/image443.gif) 的符号
的符号
+
-
+
-
数学理科.files/image445.gif) 的单调性
的单调性
ㄊ
ㄋ
ㄊ
ㄋ
由表格知:数学理科.files/image447.gif) 。………11分
。………11分
画出草图和验证数学理科.files/image449.gif) 可知,当
可知,当数学理科.files/image451.gif) 时,
时,
高考资源网版权所有数学理科.files/image453.gif)
数学理科.files/image455.gif) ……………12分
……………12分
数学理科.files/image457.gif) 函数
函数数学理科.files/image234.gif) 的图象与
的图象与数学理科.files/image236.gif) 的图象恰好有四个不同的交点. …………………13分
的图象恰好有四个不同的交点. …………………13分
21.(本小题满分13分)
解:(Ⅰ)设A数学理科.files/image459.gif) ,(
,(数学理科.files/image461.gif) )
)
∵数学理科.files/image463.gif) ,∴
,∴数学理科.files/image465.gif) ……………1分
……………1分
则A点的切线方程为数学理科.files/image467.gif)
B点的切线方程为数学理科.files/image469.gif) …………2分
…………2分
数学理科.files/image471.gif) …………3分
…………3分
数学理科.files/image473.gif) P在直线
P在直线数学理科.files/image243.gif) 上 ∴
上 ∴数学理科.files/image476.gif) =
=数学理科.files/image478.gif) , ……………4分
, ……………4分
|AF|+|BF|=数学理科.files/image480.gif)
数学理科.files/image482.gif) ……………5分
……………5分
数学理科.files/image484.gif) ……………6分
……………6分
∵数学理科.files/image476.gif) =
=数学理科.files/image478.gif) ,∴
,∴数学理科.files/image486.gif) ,当且仅当
,当且仅当数学理科.files/image488.gif) 时取等号
时取等号
∴ 数学理科.files/image245.gif) 取值范围为
取值范围为数学理科.files/image491.gif) …………8分
…………8分
(Ⅱ)∵数学理科.files/image241.gif) ,∴
,∴数学理科.files/image493.gif)
数学理科.files/image495.gif) , ……………9分
, ……………9分
设A数学理科.files/image459.gif) ,由(1)知
,由(1)知数学理科.files/image498.gif)
∴数学理科.files/image500.gif)
数学理科.files/image502.gif) …………10分
…………10分
若G在抛物线C上,则数学理科.files/image504.gif) …………11分
…………11分
数学理科.files/image506.gif) …………12分
…………12分
数学理科.files/image508.gif) ,而
,而数学理科.files/image461.gif)
数学理科.files/image511.gif)
故存在数学理科.files/image513.gif) 使G在抛物线C上。 ……………13分
使G在抛物线C上。 ……………13分
数学理科.files/image515.gif)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com