题目列表(包括答案和解析)
(本小题满分14分)
从某学校高三年级共800名男生中随机抽取50名测量身高，测量发现被测学生身高全部介于155cm和195cm之间，将测量结果按如下方式分成八组：第一组
、第二组
；…第八组
，右图是按上述分组方法得到的频率分布直方图的一部分，已知第一组与第八组人数相同，第六组、第七组、第八组人数依次构成等差数列．
(1)估计这所学校高三年级全体男生身高180cm以上（含180cm）的人数；
(2)求第六组、第七组的频率并补充完整频率分布直方图；
(3)若从身高属于第六组和第八组的所有男生中随机抽取两名男生，记他们的身高分别为
，求满足
的事件概率．
(本小题满分14分)
从某学校高一年级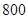
名学生中随机抽取
名测量身高，据测量被抽取的学生的身高全部介于
和
之间，将测量结果按如下方式分成八组：第一组
．第二组
；…第八组
，右图
是按上述分组方法得到的条形图．
(1)根据已知条件填写下面表格：
|
组 别 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
|
样本数 |
|
|
|
|
|
|
|
|
(2)估计这所学校高一年级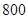名学生中身高在
以上(含)的人数；
(3)在样本中，若第二组有
人为男生，其余为女生，第七组有人为女生，其余为男生，在第二组和第七组中各选一名同学组成实验小组，问：实验小组中恰为一男一女的概率是多少？
（本小题满分14分）
某校高一年级要从3名男生
，
，
和2名女生
，
中任选3名代表参加学校的演讲比赛.学
科网
（1）求男生被选中的概率；
（2）求男生和女生至少一人被选中的概率.
.（本小题满分14分）
某校从参加高一年级期末考试的学生中抽出60名学生，将其成绩（均为整数）分成六段
，
…
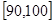后画出如下部分频率分布直方图.观察图形的信息，回答下列问题：
（1）求第四小组的频率，并补全这个频率分布直方图；
（2）估计这次考试的及格率（60分及以上为及格）和平均分；
（3）用分层抽样的方法从成绩是80分以上（包括80分）的学生中抽取了6人进行试卷分析，再从这6个人中选2人作学习经验介绍发言，求选出的2人中至少有1人在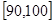的概率.
（本小题满分14分）
某校从参加高一年级期末考试的学生中抽出60名学生，并统计了他们的物理成绩（成绩均为整数且满分为100分），把其中不低于50分的分成五段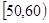
，
…
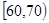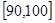后画出如下部分频率分布直方图.观察图形的信息，回答下列问题
（1）求出物理成绩低于50分的学生人数
（2）估计这次考试物理学科及格率（60分及以上为及格）
（3）从物理成绩不及格的学生中选两人，求他们成绩至少有一个不低于50分的概率.
一、填空题：（本大题共14小题，每小题5分，共70分．）
1．
； 2．
； 3．
； 4．
； 5． 11； 6． 210； 7． 16； 8． 3； 9．
； 10．
； 11． 7； 12．
； 13．
； 14．
（结果为
，不扣分）.
二、解答题：（本大题共6小题,共90分．）
15．（本小题满分14分）
解：（1）50；0.04；0.10 ． ………… 6分
（2）如图． ……………… 10分
（3）在随机抽取的
名同学中有
名
出线,
．
…………… 13分
答：在参加的
名中大概有63名同学出线．
………………… 14分
16．（本小题满分14分）
解：
真，则有
，即
．
------------------4分
真，则有
，即
．
----------------9分
若、中有且只有一个为真命题，则、一真一假．
①若真、假，则，且
，即
≤
；
----------------11分
②若假、真，则
，且，即3≤
．
----------------13分
故所求范围为：≤或3≤．
-----------------14分
17．（本小题满分15分）
解：（1）设在（1）的条件下方程
有实根为事件
．
数对
共有
对．
------------------2分
若方程有实根，则
≥
，即
． -----------------4分
则使方程有实根的数对有
共
对．
------------------6分
所以方程有实根的概率
．
------------------8分
（2）设在（2）的条件下方程有实根为事件
．
，所以
．
-------------10分
方程有实根对应区域为
，
．
--------------12分
所以方程有实根的概率
．------------------15分
18．（本小题满分15分）
解：（1）易得
．当
时，在直角
中，
，故
．所以
，
．
------------4分
所以
．
所以异面直线
与
所成角余弦值为
．- -----7分
（2）设直线
与平面
所成的角为
，平面的一个法向量为
.
则由
．得
可取
，-------11分
， 
，------------13分
，
，
． 
，
．
即直线与平面所成角的取值范围为
．
------------------------15分
19．（本小题满分16分）
解：（1）设
关于l的对称点为
，则
且
，
解得
，
，即
，故直线
的方程为
．
由
，解得
．
------------------------5分
（2）因为
，根据椭圆定义，得
，所以
．又
，所以
．所以椭圆
的方程为
．
------------------------10分
（3）假设存在两定点为
，使得对于椭圆上任意一点
（除长轴两端点）都有
（
为定值），即
?
，将
代入并整理得
…（＊）．由题意，（＊）式对任意
恒成立，所以
，解之得 
或
．
所以有且只有两定点
，使得
为定值
． ---------------16分
20．（本小题满分16分）
解：（1）
．
------------------------2分
因为
，令
得
；令
得
．所以函数的增区间为
，减区间为
．
------------------------5分
（2）因为
，设
，则
．----------6分
设切点为
，则切线的斜率为
，切线方程为
即
，由点
在切线上知
，化简得
，即
．
所以仅可作一条切线，方程是
．
------------------------9分
（3）
，．
在
上恒成立
在上的最小值
．--------------11分
①当
时，
在
上单调递减，在
上最小值为
，不符合题意，故舍去；
------------------------12分
②当
时，令
得
．
当
时，即
时，函数在上递增，的最小值为
；解得
．
------------------------13分
当
时，即
时，函数在上递减，的最小值为
，无解；
-----------------------14分
当
时，即
时，函数在
上递减、在
上递增，所以的最小值为
，无解． ------------------------15分
综上，所求
的取值范围为
．
------------------------16分
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com