
题目列表(包括答案和解析)
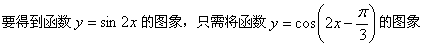
[ ]
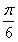 个单位
个单位 个单位
个单位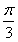 个单位
个单位  个单位
个单位 
A.向右平移 个单位长度 个单位长度 | B.向右平移 个单位长度 个单位长度 |
C.向左平移 个单位长度 个单位长度 | D.向左平移 个单位长度 个单位长度 |
由函数![]() 的图象
的图象
A.向左平移![]() 个单位 B.向左平移
个单位 B.向左平移![]() 个单位
个单位
C.向右平移![]() 个单位 D.向右平移
个单位 D.向右平移![]() 个单位
个单位
为了得到
A.向右平移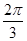 个单位长度 个单位长度 | B.向右平移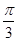 个单位长度 个单位长度 |
C.向左平移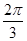 个单位长度 个单位长度 | D.向左平移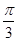 个单位长度 个单位长度 |
由函数 的图象( )
的图象( )
A.向左平移 个单位 B.向左平移
个单位 B.向左平移 个单位
个单位
C.向右平移 个单位 D.向右平移
个单位 D.向右平移 个单位
个单位
一、选择题: 本大题共12小题,每小题5分,共60分.
题号
1
2
3
4
5
6
7
8
9
10
11
12
答案
C
B
C
D
B
C
A
D
C
D
B
B
二、填空题:本大题共4小题,每小题4分,共16分.
13. 14.
14. 15.
15. 16.
16.
三、解答题:本大题共6小题,共74分.解答应写出文字说明、证明过程或演算步骤.
17.(本小题满分12分)
解:⑴f (x)= ?
? -1=(
-1=( sin2x,cosx)?(1,2cosx)-1
sin2x,cosx)?(1,2cosx)-1
= sin2x+2cos2x-1=
sin2x+2cos2x-1= sin2x+cos2x=2sin(2x+
sin2x+cos2x=2sin(2x+ )
3分
)
3分
由2kπ- ≤2x+
≤2x+ ≤2kπ+
≤2kπ+ 得kπ-
得kπ- ≤x≤kπ+
≤x≤kπ+
∴f (x)的递增区间为 (k∈Z)
6分
(k∈Z)
6分
⑵f (A)=2sin( )=2 ∴sin(
)=2 ∴sin( )=1
)=1
∴ =
= ∴A=
∴A= 9分
9分
由正弦定理得:  .∴边长b的值为
.∴边长b的值为 .
12分
.
12分
18.(本小题满分12分)
解: 将一颗骰子先后抛掷2次,此问题中含有36个等可能基本事件 1分
(1)记“两数之和为
所以P(A)= ;
;
答:两数之和为5的概率为 . 4分
. 4分
(2)记“两数中至少有一个奇数”为事件B,则事件B与“两数均为偶数”为对立事件,
所以P(B)= ;
;
答:两数中至少有一个奇数的概率 .
8分
.
8分
(3)基本事件总数为36,点(x,y)在圆x2+y2=15的内部记为事件C,则C包含8个事件,
所以P(C)= .
.
答:点(x,y)在圆x2+y2=15的内部的概率 .
12分
.
12分
19.(本小题满分12分)
 (1)证法1:如图,取
(1)证法1:如图,取 的中点
的中点 ,连接
,连接 ,
,
∵ 分别为
分别为 的中点,∴
的中点,∴ .
.
∵ 分别为
分别为 的中点,∴
的中点,∴ .
.
∴
 .
.
∴ 四点共面.………………………………………………………………2分
四点共面.………………………………………………………………2分
∵ 分别为
分别为 的中点,∴
的中点,∴ .……………………………………4分
.……………………………………4分
∵ 平面
平面 ,
, 平面
平面 ,
,
∴ 平面
平面 .……………………………………………………………………6分
.……………………………………………………………………6分
证法2:∵ 分别为
分别为 的中点,
的中点,
∴ ,
, .……………………………………………………………2分
.……………………………………………………………2分
∵ ,∴
,∴ .又
.又
 …………………4分
…………………4分
∵ ,∴平面
,∴平面 平面
平面 . …………………5分
. …………………5分
∵ 平面
平面 ,∴
,∴ 平面
平面 . …………………………………………6分
. …………………………………………6分
(2)解:∵ 平面
平面 ,
, 平面
平面 ,∴
,∴ .
.
∵ 为正方形,∴
为正方形,∴ .
.
∵ ,∴
,∴ 平面
平面 .……………………………………………8分
.……………………………………………8分
∵ ,
, ,∴
,∴ .……………10分
.……………10分
∵ ,
,
∴ .…………………………………12分
.…………………………………12分
20.(本小题满分12分)
解:(1)∵
 …………………2分
…………………2分
(2)证明:

 是以
是以
 为首项,2为公比的等比数列. ………………7分
为首项,2为公比的等比数列. ………………7分
(3)由(I)得

 ………………12分
………………12分
21.(本小题满分12分)
解:(1)设切线的斜率为k,则 ………2分
………2分
又 ,所以所求切线的方程为:
,所以所求切线的方程为: …………4分
…………4分
即 …………6分
…………6分
(2) , ∵
, ∵ 为单调增函数,∴
为单调增函数,∴
即对任意的 …………8分
…………8分

 …………10分
…………10分
而 ,当且仅当
,当且仅当 时,等号成立.
时,等号成立.
所以 …………12分
…………12分
22.(本小题满分14分)
解:(1)由题意设椭圆的标准方程为 ,
,
由已知得: …………3分
…………3分
 椭圆的标准方程为
椭圆的标准方程为 .
…………5分
.
…………5分
(2)设 .
.
联立 得:
得: , …………6分
, …………6分
则  …………8分
…………8分
又 .
.
因为以 为直径的圆过椭圆的右顶点
为直径的圆过椭圆的右顶点 ,
,
 ,即
,即 .
…………9分
.
…………9分
 .
.
 .
.
 .
…………10分
.
…………10分
解得: ,且均满足
,且均满足 .
…………11分
.
…………11分
当 时,
时, 的方程
的方程 ,直线过点
,直线过点 ,与已知矛盾;…………12分
,与已知矛盾;…………12分
当 时,
时, 的方程为
的方程为 ,直线过定点
,直线过定点 . …………13分
. …………13分
所以,直线 过定点,定点坐标为
过定点,定点坐标为 .
…………14分
.
…………14分
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com