查看答案和解析>>

若直线y=kx+1与圆x²+y²=1相交于P、Q两点，且∠POQ=120°(其中O为原点)，则k的值为(　　)

A．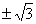

B．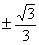

C．±1

D．不存在

查看答案和解析>>

已知圆O：x²+y²=2交x轴于A，B两点，曲线C是以AB为长轴，离心率为

2

2

的椭圆，其左焦点为F．若P是圆O上一点，连接PF，过原点O作直线PF的垂线交椭圆C的左准线于点Q．
（1）求椭圆C的标准方程；
（2）若点P的坐标为（1，1），求证：直线PQ与圆O相切；
（3）试探究：当点P在圆O上运动时（不与A、B重合），直线PQ与圆O是否保持相切的位置关系？若是，请证明；若不是，请说明理由．

查看答案和解析>>

已知圆O：x2+y2=

4

9

，直线l：y=kx+m与椭圆C：

x2

2

+y2=1相交于P、Q两点，O为原点．
（Ⅰ）若直线l过椭圆C的左焦点，且与圆O交于A、B两点，且∠AOB=60°，求直线l的方程；
（Ⅱ）如图，若△POQ重心恰好在圆上，求m的取值范围．

查看答案和解析>>

查看答案和解析>>

1．C  2．D  3．A  4．A  5．C  6．D  7．D  8．A 9．C10.D   11.B12.D

13．

14．

15．

16．  

17

18．解：

 ⑴ .

⑵ 函数在上单调递增，

在上单调递减.

所以,当时，；当时，.

故的值域为.

19．解：由题意可知圆的方程为，于是.

时，设，，则由得,

，. 所以的中点坐标为.

又由,且,可知直线与直线垂直，即直线的斜率为.

此时直线的方程为,即.

时,同理可得直线的方程为.

故直线的方程为 或 .

20. 解：（Ⅰ）设这二次函数f(x)＝ax²+bx (a≠0) ,则 f`(x)=2ax+b,由于f`(x)=6x－2,得

a=3 ,  b=－2, 所以  f(x)＝3x²－2x.

又因为点均在函数的图像上，所以＝3n²－2n.

当n≥2时，a_n＝S_n－S_n－1＝（3n²－2n）－

＝6n－5.

当n＝1时，a₁＝S₁＝3×1²－2＝6×1－5，所以，a_n＝6n－5 （）

（Ⅱ）由（Ⅰ）

得知＝＝，

故T_n＝＝

＝（1－

因此，要使（1－）<（）成立的m,必须且仅须满足≤，即m≥10，所以满足要求的最小正整数m为10.

21.解：⑴设，∵不等式的解集为

∴ ……… ①       ……… ②

又∵有两等根，

∴……… ③     由①②③解得   …………（5分）

又∵，

∴，故.

∴  …………………………（7分）

⑵由①②得，

∴，

……………………（9分）

∵无极值，∴方程

       ，

解得  …………（12分）

22.(1);

   (2)

   (3)