
题目列表(包括答案和解析)
设函数 ,则下列结论正确的是( )
,则下列结论正确的是( )
A. 的图像关于直线
的图像关于直线 对称
对称
B. 的图像关于点
的图像关于点 对称
对称
C. 的最小正周期为
的最小正周期为 ,且在
,且在 上为增函数
上为增函数
D.把 的图像向右平移
的图像向右平移 个单位,得到一个偶函数的图像
个单位,得到一个偶函数的图像
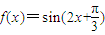 ,则下列结论正确的是( )
,则下列结论正确的是( ) 为减函数
为减函数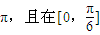 上为增函数
上为增函数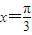 对称
对称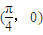 对称
对称设函数 ,则下列结论正确的是
,则下列结论正确的是
A. 的图像关于直线
的图像关于直线 对称
对称
B. 的图像关于点
的图像关于点 对称
对称
C. 的最小正周期为
的最小正周期为 ,且在
,且在 上为增函数
上为增函数
D.把 的图像向右平移
的图像向右平移 个单位,得到一个偶函数的图像
个单位,得到一个偶函数的图像
一、选择题 CAAD ABDAB CB
二、填空题  .
.
 .
.
 .
.
 .
.

三、解答题
 .
.





 的周期为
的周期为 ,最大值为
,最大值为 .
.
 由
由 得
得 ,
,
又 ,
, ,
,
∴ 或
或 或
或
∴ 或
或  或
或 
 .
. 显然事件
显然事件 即表示乙以
即表示乙以 获胜,
获胜,
∴

 的所有取值为
的所有取值为 .
.



∴ 的分布列为:
的分布列为:

3
4
5




数学期望 .
.
 .
. 当
当 在
在 中点时,
中点时, 平面
平面 .
.
 延长
延长 、
、 交于
交于 ,则
,则 ,
,
连结 并延长交
并延长交 延长线于
延长线于 ,
,
则 ,
, .
.
在 中,
中, 为中位线,
为中位线, ,
,
又 ,
,
∴ .
.
 ∵
∵ 中,
中,
∴ ,即
,即
又 ,
, ,
,
∴ 平面
平面 ∴
∴ .
.
∴ 为平面
为平面 与平面
与平面 所成二面
所成二面
角的平面角。
又 ,
,
∴所求二面角的大小为 .
.
 .
. 由题意知
由题意知 的方程为
的方程为 ,设
,设 ,
, .
.
联立 得
得 .
.
∴ .
.
由抛物线定义 ,
,
∴ .抛物线方程
.抛物线方程 ,
,
 由题意知
由题意知 的方程为
的方程为 .设
.设 ,
,
则 ,
, ,
,
∴
 .
.
由 知
知 ,
, ,
, ,
, .
.
则
∴当 时,
时, 的最小值为
的最小值为
 .
.
 .
. ∵
∵
 ,
,
∴ .
.
∴
∴
即
∴ s
s


 时,也成立
时,也成立
∴

 ,
,
∴

∴


∵
 ,
,
又




∴
 .
.
 ,
,
∵ 在
在 上单调,
上单调,
∴ 或
或 在
在 上恒成立.
上恒成立.
即 或
或 恒成立.
恒成立.
 或
或 在
在 上恒成立.
上恒成立.
又 ,
,
∴ 或
或 .
.
 由
由 得:
得:
 ,
,
化简得
当 时,
时, ,
, ,
,
∴
又 ,
,
∴
当 时,
时, ,
,
综上,实数 的取值范围是
的取值范围是
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com