
题目列表(包括答案和解析)
第一象限内有一动点 ,在过点
,在过点 且方向向量
且方向向量 的直线上运动,则
的直线上运动,则 的最大值为________________________
的最大值为________________________
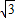 ,求直线l的方程;
,求直线l的方程;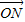 =(0,y),若向量
=(0,y),若向量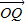 =
=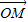 +
+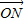 ,求动点Q的轨迹方程.
,求动点Q的轨迹方程.已知圆C的方程为:x2+y2=4.
(1)求过点P(1,2)且与圆C相切的直线l的方程;
(2)直线l过点P(1,2),且与圆C交于A、B两点,若|AB|=2![]() ,求直线l的方程;
,求直线l的方程;
(3)圆C上有一动点M(x0,y0),![]() =(0,y0),若向量
=(0,y0),若向量![]() =
=![]() +
+![]() ,求动点Q的轨迹方程,并说明此轨迹是什么曲线.
,求动点Q的轨迹方程,并说明此轨迹是什么曲线.
| 3 |
| ON |
| OQ |
| OM |
| ON |
一、选择题 CAAD ABDAB CB
二、填空题  .
.
 .
.
 .
.
 .
.

三、解答题
 .
.





 的周期为
的周期为 ,最大值为
,最大值为 .
.
 由
由 得
得 ,
,
又 ,
, ,
,
∴ 或
或 或
或
∴ 或
或  或
或 
 .
. 显然事件
显然事件 即表示乙以
即表示乙以 获胜,
获胜,
∴

 的所有取值为
的所有取值为 .
.



∴ 的分布列为:
的分布列为:

3
4
5




数学期望 .
.
 .
. 当
当 在
在 中点时,
中点时, 平面
平面 .
.
 延长
延长 、
、 交于
交于 ,则
,则 ,
,
连结 并延长交
并延长交 延长线于
延长线于 ,
,
则 ,
, .
.
在 中,
中, 为中位线,
为中位线, ,
,
又 ,
,
∴ .
.
 ∵
∵ 中,
中,
∴ ,即
,即
又 ,
, ,
,
∴ 平面
平面 ∴
∴ .
.
∴ 为平面
为平面 与平面
与平面 所成二面
所成二面
角的平面角。
又 ,
,
∴所求二面角的大小为 .
.
 .
. 由题意知
由题意知 的方程为
的方程为 ,设
,设 ,
, .
.
联立 得
得 .
.
∴ .
.
由抛物线定义 ,
,
∴ .抛物线方程
.抛物线方程 ,
,
 由题意知
由题意知 的方程为
的方程为 .设
.设 ,
,
则 ,
, ,
,
∴
 .
.
由 知
知 ,
, ,
, ,
, .
.
则
∴当 时,
时, 的最小值为
的最小值为
 .
.
 .
. ∵
∵
 ,
,
∴ .
.
∴
∴
即
∴ s
s


 时,也成立
时,也成立
∴

 ,
,
∴

∴


∵
 ,
,
又




∴
 .
.
 ,
,
∵ 在
在 上单调,
上单调,
∴ 或
或 在
在 上恒成立.
上恒成立.
即 或
或 恒成立.
恒成立.
 或
或 在
在 上恒成立.
上恒成立.
又 ,
,
∴ 或
或 .
.
 由
由 得:
得:
 ,
,
化简得
当 时,
时, ,
, ,
,
∴
又 ,
,
∴
当 时,
时, ,
,
综上,实数 的取值范围是
的取值范围是
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com