
题目列表(包括答案和解析)
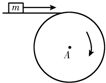 m为在水平传送带上被传送的小物体(可视为质点),A为终端皮带轮,如图所示,已知皮带轮半径为r,传送带与皮带轮间、传送带与小物体间不会打滑.当m可被水平抛出时,
m为在水平传送带上被传送的小物体(可视为质点),A为终端皮带轮,如图所示,已知皮带轮半径为r,传送带与皮带轮间、传送带与小物体间不会打滑.当m可被水平抛出时,m为在水平传送带上被传送的小物体(可视为质点),A为终端皮带轮,如图所示,已知皮带轮半径为r,传送带与皮带轮间不会打滑。当m可被水平抛出时,A 轮每秒的转速最少是( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
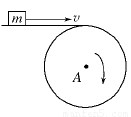
m为在水平传送带上被传送的小物体(可视为质点),A为终端皮带轮,如图所示,已知皮带轮半径为r,传送带与皮带轮间、传送带与小物体间不会打滑,当m可被水平抛出时,求:
【小题1】 A轮每秒的转数n最少是多少?
【小题2】若A轮有上述的最小转速,且其最高点距地面高度为h,求小物体落地的速度方向(用反三角函数表示).
m为在水平传送带上被传送的小物体(可视为质点),A为终端皮带轮,如图所示,已知皮带轮半径为r,传送带与皮带轮间、传送带与小物体间不会打滑.当m可被水平抛出时,

(1)A轮每秒的转数n最少是多少?
(2)若A轮有上述的最小转速,且其最高点距地面高度为h,求小物体落地的速度方向(用反三角函数表示)
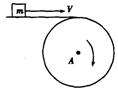
m为在水平传送带上被传送的小物体(可视为质点),A为终端皮带轮,如图所示,已知皮带轮半径为r,传送带与皮带轮间不会打滑.当m可被水平抛出时.A轮每秒的转速最少是( )

一、单项选择题
1-4DABD
二、多项选择题
5、ABD 6、AD 7、BC 8、BD
三、实验题
9.10.5 1.731(1.730~1.733均给分)
10.(1)C (2)如图

(3)法一
a.
b.如图
c.纵轴截距的倒数 斜率除以纵轴的截距
法二
a.
b.如图
c.斜率除以纵轴截距的绝对值 纵轴截距的倒数的绝对值
11.A题:
 (1)1,-x方向
(1)1,-x方向
(2)解:①光在圆柱体中的传播速度

②设光线PC经折射后经过B点,光路图如图所示
由折射定律有:
又由几何关系有: 
解①②得 
光线PC离直线AB的距离CD=Rsinα=10 cm
cm
则距离直线AB cm
cm
B题:
(1)AD
(2)子弹射入木块瞬间动量守恒
mv0=(M+m)v
得 v=mv0/(M+m)
子弹和木块一起上升,上升过程只有重力做功,机械能守恒,则有


12.Fcos -
- N = ma
(1)
N = ma
(1)
Fsin +N=mg (2)
+N=mg (2)
a>0 (3)
N≥0 (4)
由(1)(2)(3)(4)得 <F≤
<F≤ 。
。
13.解:(1)在14s―18s时间段加速度
a=6/(18―14)=
Ff=ma=1.0×1.5N=1.5N
(2)在5s―7s小车作匀速运动,牵引力F=Ff
P=Fv=1.5×6W=9W
(3)0―2s内x1= ×2×
×2×
2s―10s内根据动能定理
Pt―Ffx2= mv
mv ―
―
解得
x2=
加速过程中小车的位移大小为
x=x1+x2=
14.(1)粒子在电场中被加速,由动能定理得
qU=
 粒子在磁场中偏转,则牛顿第二定律得
粒子在磁场中偏转,则牛顿第二定律得
qvB=m
联立解得
r=
=
=
(2)由几何关系可得, 粒子恰好垂直穿过分界线,故正确图象为
粒子恰好垂直穿过分界线,故正确图象为

(3)带电粒子在磁场中的运动周期

 粒子在两个磁场中分别偏转的弧度为
粒子在两个磁场中分别偏转的弧度为 ,在磁场中的运动总时间
,在磁场中的运动总时间
t=
=
=6.5×10―6(s)
15.(1) I=
I=
因为金属棒始终静止,在t时刻磁场的磁感应强度为Bt=B0+kt,所以
F外=FA=BIl=(B0+kt) =
=

方向向右
(2)根据感应电流产生的条件,为使回路中不产生感应电流,回路中磁通量的变化应为零,因为磁感强度是逐渐增大的,所以金属棒应向左运动(使面积减小)
即: =0,即
=0,即 =BtSt―B0S0,
=BtSt―B0S0,
也就是Btl(l― )=B
)=B
得Bt=
(3)如果金属棒向右匀速运动,因为这时磁感应强度是逐渐减小的,同理可推得,

所以磁感应强度随时间变化的图像如图(t1时刻Bt不为零)

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com