如图甲所示，在坐标系xoy中，y轴左侧有沿x轴正向的匀强电场，场强大小为E；y轴右侧有如图乙所示，大小和方向周期性变化的匀强磁场，磁感强度大小B₀已知．磁场方向垂直纸面向里为正．t=0时刻，从x轴上的p点无初速释放一带正电的粒子，质量为m，电量为q（粒子重力不计），粒子第一次在电场中运动时间与第一次在磁场中运动的时间相等．求

（1）P点到O点的距离；
（2）粒子经一个周期沿y轴发生的位移；
（3）粒子能否再次经过O点，若不能说明理由．若能，求粒子再次经过O点的时刻；
（4）粒子第4n（n=1、2、3…）次经过y轴时的纵坐标．

查看答案和解析>>

查看答案和解析>>

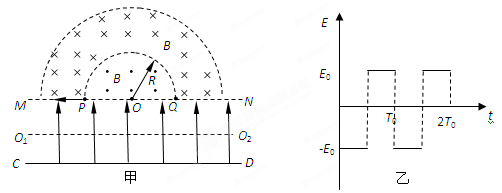
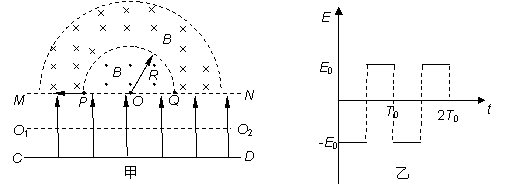
如图甲所示，CD和MN之间存在着变化的电场，电场变化规律如图乙所示（图中电场方向为正方向），MN为一带电粒子可以自由通过的理想边界，直线MN下方无磁场，上方两个同心半圆内存在着有理想边界的匀强磁场，其分界线是半径为R和2R的半圆，半径为R的圆两侧的磁场方向相反且垂直于纸面，磁感应强度大小都为B。现有一质量为m、电荷量为q的带负电微粒在t=0时刻从O₂点沿MN、CD间的中心线O₂O₁水平向左射入电场，到达P点时以水平向左的速度进入磁场，最终打在Q点。不计微粒的重力。求：
（1）微粒在磁场中运动的周期T；
（2）微粒在电场中的运动时间t₁与电场的变化周期T₀之间的关系；
（3）MN、CD之间的距离d；
（4）微粒在磁场中运动的半径r的可能值的表达式及r的最大值。

查看答案和解析>>

如图甲所示，一对平行放置的金属板M、N的中心各有一小孔P、Q，PQ连线垂直于金属板；N板右侧的圆A内分布有方向垂直于纸面的匀强磁场，磁感应强度大小为B，圆半径为r，且圆心O在PQ的延长线上，现使置于P处的粒子源连续不断地沿PQ方向放出质量为m、电量为q的带电粒子（带电粒子的重力和初速度忽略不计，粒子间的相互作用力忽略不计），从某一时刻开始，在板M、N 间加上如图乙所示的交变电压，周期为T，电压大小为U，如果只有在每个周期的0～T/4时间内放出的带电粒子才能从小孔Q中射出，求：
（1）带电粒子到达Q孔可能的速度范围；
（2）带电粒子通过该圆形磁场的最小偏转角θ。

查看答案和解析>>

查看答案和解析>>

一、本题共12小题，全部为必做题。每小题4分，共48分.在每小题给出的四个选项中，有的小题只有一个选项正确，有的小题有多个选项正确.全部选对的得4分，选不全的得2分，有选错或不答的得0分.

题号

1

2

3

4

5

6

7

8

9

10

11

12

答案

C

C

A

BD

C

B

BD

B

C

BD

AC

BC

二、 本题共7小题，共102分.全部为必做题，请按题目要求作答.解答题应写出必要的文字说明、方程式和重要演算步骤.只写出最后答案的不能得分.有数值计算的题，答案中必须明确写出数值和单位.

13、（12分）（1）①，物体质量的倒数；②，（当地）重力加速度g；（每空1分）

（2）①表格如下：（3分）

位置

1

2

3

4

5

6

t/s

s/m

②  t  t²   （每空1分）

处理方法：尝试作出s―t图，看是否是直线，若不是再作出s―t²图。（3分）

14、（共12分，每小题4分） （1）×100Ω；   3.0 KΩ     

（2）乙 ；   因为甲图中流过电流表的电流太小，读数误差比较大 

（3）K₂闭合前后电压表的读数U₁、U₂   ；

15、（10分）解：对B受力分析的绳中拉力T=m_B g；               （1分）

当m_B取最大值时，物体具有沿斜面向下的最大静摩擦力f_m；

对A受力分析并正交分解得：     N－mgcosθ=0；                （1分）

T－f_m－mgsinθ=0；             （1分）

f_m=μN                         （1分）

联立以上各式，解得：           m_B=m(sinθ+μcosθ)               （1分）

当m_B取最小值时，物体具有沿斜面向上的最大静摩擦力f_m；

对A受力分析并正交分解得：     N－mgcosθ=0；                （1分）

T+f_m－mgsinθ=0；              （1分）

f_m=μN                         （1分）

联立以上各式，解得：           m_B=m(sinθ－μcosθ)              （1分）

综上，m_B的范围是： m(sinθ－μcosθ)≤m_B≤m(sinθ+μcosθ)            （1分）

16．(1)（8分）解：（1）由，得：         （3分）

由，          （4分）

整理得：                                     （1分）

评分标准：中间字母脚标错的一律不给分。

16．（10分）

(2)设A、B的质量分别为m_A、m_B，长木板B长度为L，A、B之间的滑动摩擦力为f.

=fL                         ①（2分）

若B不固定，对A、B系统由动量守恒，有

m_Av₀=(m_A+m_B)v                      ②（3分）

对A、B系统由能量守恒，有

=fL+(m_A+m_B)v²              ③（3分）

由以上各式解得：=                           ④（2分）

17．（17分）解：（1）做加速度减小的减速运动直到停止运动。 （3分）

               图象如答图1                              （2分）

（2）金属杆在导轨上做减速运动，刚开始时速度最大，感应电动势也最大，有：                E_m = BLv₀                            （1分）

所以回路的最大电流I_m =  ．                          （2分）

金属杆上电流方向从a到b                      （1分）

（3）   E = BLv                                     （1分）   

F= BIL                                      （1分）

由闭合电路欧姆定律得：I =                （1分）

由牛顿第二定律得：F = ma                     （1分）

解得：a =  B ²L² v / (mR)                       （2分）

         （4）：  由能的转化和守恒有： Q = mv²₀         （2分）

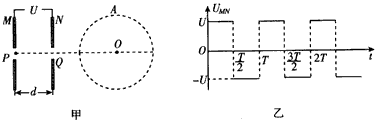
18、（17分）解：如答图2。（1）设粒子过N点时速度v，有：

＝cosθ　　　   ①       （1分）

v＝2v₀            ②       （1分）

粒子从M点运动到N点的过程，有：

qU_MN＝mv²－mv　      ③       （2分）

U_MN＝　　　　　　　　　④        （1分）

（2）粒子在磁场中以O^/为圆做匀速圆周运动，半径为O^/N，有

qvB＝             ⑤    （1分）  

r＝　　　　　　  ⑥     （1分）

（3）由几何关系得：           ON＝rsinθ             ⑦     （2分）

  粒子在电场中运动的时间t₁，有：ON＝v₀t₁              ⑧       （1分）

t₁＝　　　        ⑨      （1分）

粒子在磁场中做匀速圆周运动的周期：T＝　　　　　　⑩     （1分）

设粒子在磁场中运动的时间t₂，有：t₂＝            ⑾     （2分）

t₂＝　　　        ⑿      （1分）

                      t＝t₁＋t₂t＝　 　⒀    （2分）

19. （16分）解：（1）当A、B、C三者的速度相等时（设为v₁），弹簧的弹性势能最大，由于A、B、C三者组成的系统动量守恒，

    ①                 （2分）

       解得：　　　　　 ②                   （2分）

  （2）B、C碰撞时B、C组成的系统动量守恒，设碰后瞬间B、C两者速度为v₂，则

                           ③　　

解得：　　        ④                   （2分）

设弹性势能的最大值为，由机械能守恒得：

  　⑤        （3分）

代入数值得：   　　　　　                          ⑥        （1分）

（3）A不可能向左运动。由系统的动量守恒：

　            ⑦         （1分）

 若A向左运动，，则　　        ⑧　        （2分 ）

此时系统的动能之和：

⑨      （1分）

而系统的机械能：　⑩      （1分）

根据能量守恒是不可能的。                                         （1分）