
题目列表(包括答案和解析)
 已知△OFQ的面积为2
已知△OFQ的面积为2| 6 |
| OF |
| FQ |
| 6 |
| 6 |
| OF |
| FQ |
| OF |
| ||
| 4 |
| OQ |
 的渐近线方程为
的渐近线方程为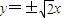 ;
;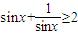 ”是真命题;
”是真命题;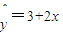 ,当变量x增加2个单位,其预报值平均增加4个单位;
,当变量x增加2个单位,其预报值平均增加4个单位;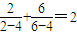 ,
,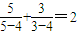 ,
,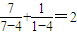 ,
,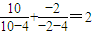 ,依照以上各式的规律,得到一般性的等式为
,依照以上各式的规律,得到一般性的等式为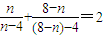 ,(n≠4)
,(n≠4)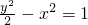 的渐近线方程为
的渐近线方程为 ;
;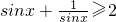 ”是真命题;
”是真命题;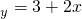 ,当变量x增加2个单位,其预报值平均增加4个单位;
,当变量x增加2个单位,其预报值平均增加4个单位;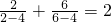 ,
,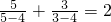 ,
,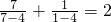 ,
,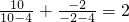 ,依照以上各式的规律,得到一般性的等式为
,依照以上各式的规律,得到一般性的等式为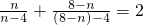 ,(n≠4)
,(n≠4)| y2 |
| 2 |
| 2 |
| 1 |
| sinx |
| ? |
| y |
| 2 |
| 2-4 |
| 6 |
| 6-4 |
| 5 |
| 5-4 |
| 3 |
| 3-4 |
| 7 |
| 7-4 |
| 1 |
| 1-4 |
| 10 |
| 10-4 |
| -2 |
| -2-4 |
| n |
| n-4 |
| 8-n |
| (8-n)-4 |
| y2 |
| 2 |
| 2 |
| 1 |
| sinx |
| ? |
| y |
| 2 |
| 2-4 |
| 6 |
| 6-4 |
| 5 |
| 5-4 |
| 3 |
| 3-4 |
| 7 |
| 7-4 |
| 1 |
| 1-4 |
| 10 |
| 10-4 |
| -2 |
| -2-4 |
| n |
| n-4 |
| 8-n |
| (8-n)-4 |
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com