
题目列表(包括答案和解析)
 如图1:等边
如图1:等边 可以看作由等边
可以看作由等边 绕顶点
绕顶点 经过旋转相似变换得到.但是我们注意到图形中的
经过旋转相似变换得到.但是我们注意到图形中的 和
和 的关系,上述变换也可以理解为图形是由
的关系,上述变换也可以理解为图形是由 绕顶点
绕顶点 旋转
旋转 形成的.于是我们得到一个结论:如果两个正三角形存在着公共顶点,则该图形可以看成是由一个三角形绕着该顶点旋转
形成的.于是我们得到一个结论:如果两个正三角形存在着公共顶点,则该图形可以看成是由一个三角形绕着该顶点旋转 形成的.
形成的.
① 利用上述结论解决问题:如图2, 中,
中, 都是等边三角形,求四边形
都是等边三角形,求四边形 的面积;
的面积;
② 图3中,  ∽
∽ ,
, ,仿照上述结论,推广出符合图3的结论.(写出结论即可)
,仿照上述结论,推广出符合图3的结论.(写出结论即可)
如图1:等边 可以看作由等边
可以看作由等边 绕顶点
绕顶点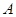 经过旋转相似变换得到.但是我们注意到图形中的
经过旋转相似变换得到.但是我们注意到图形中的 和
和 的关系,上述变换也可以理解为图形是由
的关系,上述变换也可以理解为图形是由 绕顶点
绕顶点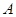 旋转
旋转 形成的.于是我们得到一个结论:如果两个正三角形存在着公共顶点,则该图形可以看成是由一个三角形绕着该顶点旋转
形成的.于是我们得到一个结论:如果两个正三角形存在着公共顶点,则该图形可以看成是由一个三角形绕着该顶点旋转 形成的.
形成的.

① 利用上述结论解决问题:如图2, 中,
中, 都是等边三角形,求四边形
都是等边三角形,求四边形 的面积;
的面积;
② 图3中,  ∽
∽ ,
, ,仿照上述结论,推广出符合图3的结论.(写出结论即可)
,仿照上述结论,推广出符合图3的结论.(写出结论即可)
 如图1:等边
如图1:等边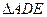 可以看作由等边
可以看作由等边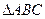 绕顶点
绕顶点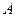 经过旋转相似变换得到.但是我们注意到图形中的
经过旋转相似变换得到.但是我们注意到图形中的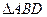 和
和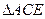 的关系,上述变换也可以理解为图形是由
的关系,上述变换也可以理解为图形是由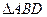 绕顶点
绕顶点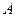 旋转
旋转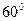 形成的.于是我们得到一个结论:如果两个正三角形存在着公共顶点,则该图形可以看成是由一个三角形绕着该顶点旋转
形成的.于是我们得到一个结论:如果两个正三角形存在着公共顶点,则该图形可以看成是由一个三角形绕着该顶点旋转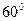 形成的.
形成的.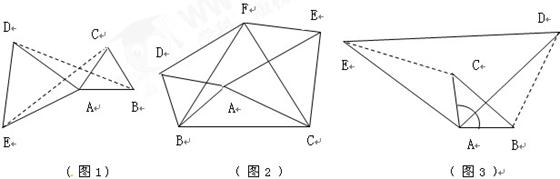
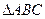 中,
中,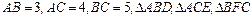 都是等边三角形,求四边形
都是等边三角形,求四边形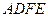 的面积;
的面积;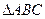 ∽
∽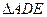 ,
,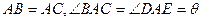 ,仿照上述结论,推广出符合图3的结论.(写出结论即可)
,仿照上述结论,推广出符合图3的结论.(写出结论即可)为了更好地了解鲸的生活习性,某动物保护组织在受伤的鲸身上安装了电子监测装置,从海岸放归点A处(如图所示)把它放归大海,并沿海岸线由西到东不停地对鲸进行了长达40分钟的跟踪观测,每隔10分钟踩点测得数据如下表(没鲸沿海面游动),然后又在观测站B处对鲸进行生活习性的详细观测.已知AB=15km,观测站B的观测半径为5km.

(1)据表中信息:①计算出鲸沿海岸线方向运动的速度,②度写出a、近似满足的关系式并画出鲸的运动路线草图;
(2)若鲸继续以(1)②中运行路线运动,试预测,该鲸经过多长时间(从放归时计是时),可进入前方观测站B的观测范围?并求出可持续观测的时间.(注 精确到1分钟)
精确到1分钟)



湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com