
题目列表(包括答案和解析)
(1)由“若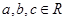 则
则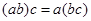 ”类比“若
”类比“若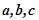 为三个向量则
为三个向量则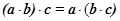 ”
”
(2)在数列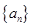 中,
中,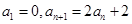 猜想
猜想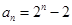
(3)在平面内“三角形的两边之和大于第三边”类比在空间中“四面体的任意三个面的
面积之和大于第四个面的面积”
(4)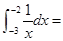
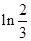
上述四个推理中,得出的结论正确的是______.(写出所有正确结论的序号)
(1)由“若![]() 则
则![]() ”类比“若
”类比“若![]() 为三个向量则
为三个向量则![]() ”
”
(2)在数列![]() 中,
中,![]() 猜想
猜想![]()
(3)在平面内“三角形的两边之和大于第三边”类比在空间中“四面体的任意三个面的
面积之和大于第四个面的面积”
(4)![]()
![]()
上述四个推理中,得出的结论正确的是______.(写出所有正确结论的序号)
若平行四边形三个顶点的坐标为(1,0),(5,8),(7,-4),则第四个顶点坐标为 。
若平行四边形三个顶点的坐标为(1,0),(5,8),(7,-4),则第四个顶点坐标为 。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com