
题目列表(包括答案和解析)
已知等差数列{an}中,Sn表示其前n项和,且S1=1,S19=95,则a19=________,S10=________.
| 用Sm表示S2m | S2m=2Sm+m2d |
用 、 、 表示 表示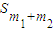 |  =______① =______① |
| 用Sm表示Snm | Snm=______② |
| 2 |
| 2 |
| 2 |
| Sn |
| n |
一、选择题(本大题共8小题,每小题5分,共40分)
题号
(1)
(2)
(3)
(4)
(5)
(6)
(7)
(8)
答案
B
A
C
B
D
B
C
A
二、填空题(本大题共6小题,每小题5分,共30分.第一个空3分,第二个空2分)
(9)±3(丢一个不给分) (10)10 (11)
(12)9,30 (13)34 (14)(-2 ,2
,2 ),(-∞,3]
),(-∞,3]
三、解答题(本大题共6小题,共80分.解答应写出文字说明,证明过程或演算步骤)
(15)(本小题满分12分)
解:(Ⅰ)由 <0.
<0.
得-2<x<2.
∴A={x|-2<x<2}.……………………………………………………………3分
由|x-2|<1.
得1<x<3.
∴B={x|l<x<3}.…………………………………………………………………6分
(Ⅱ)∵A={x|-2<x<2},U=R,
∴ UA={x|x≤-2或x≥2}.……………………………………………………9分
UA={x|x≤-2或x≥2}.……………………………………………………9分
∴( U A)∩B={x|2≤x<3}.……………………………………………………12分
U A)∩B={x|2≤x<3}.……………………………………………………12分
(16)(本小题满分13分)
解:(Ⅰ)由f (x)=x3+ax2+2得
f ′ (x)=3x2+2ax.………………………………………………………………………………3分
∵f ′ (x)图象关于直线x=l对称,
∴- =1.
=1.
∴a=-3.……………………………………………………………………………………6分
(Ⅱ)由(Ⅰ)知f (x)=x3-3x2+2,f ′ (x)=3x2-6x.
令f ′ (x)=0得x1=0,x2=2.……………………………………………………………8分
当x在[-1,2]上变化时,f ′ (x),f (x)的变化情况如下表
x
-1
(-1,0)
0
(0,2)
2
f ′ (x)
+
0
-
0
f (x)
-2
ㄊ
2
ㄋ
-2
……………………………………………………………………………………………12分
由上表可知,当x=-1或2时,函数有最小值-2,当x=0时,函数有最大值2.
……………………………………………………………………………………………13分
(17)(本小题满分14分)
解:(Ⅰ)设任取一件作品颜色为绿色的事件为A. ………………………………………1分
P(A)= .…………………………………………………………………………………
4分
.…………………………………………………………………………………
4分
答:任取一件作品颜色为绿色的概率为 .
.
(Ⅱ)设任取一件作品颜色为红色的事件为B ……………………………………………5分
P(B)=1- …………………………………………………………………………
7分
…………………………………………………………………………
7分
=l- =
= .……………………………………………………………………………… 8分
.……………………………………………………………………………… 8分
答:任取一件作品颜色为红色的概率为 .
.
(Ⅲ)设任取一件作品记下颜色后放回,连续取三次至少有两件作品为红色的
事件为C.……………………………………………………………………………………9分
P(C)= (
( )2(
)2( )+
)+ (
( )3(
)3( )0………………………………13分(其中两个算式各2分)
)0………………………………13分(其中两个算式各2分)
= .…………………………………………………………………………………14分
.…………………………………………………………………………………14分
答:任取一件作品记下颜色后放回,连续取三次至少有两件作品为红色的概率为 .
.
(18)(本小题满分13分)
解:(Ⅰ)∵a1=-1,且an=3an-l-2n+3,(n=2,3,…)
∴a2=3al-4+3=-4,…………………………………………………………… 2分
a3=
当n≥2时,有
an-n=3an-1-2n+3-n=3(an-1-n+1) …………………………………………6分
且a1-1=-2≠0,…………………………………………………………………7分
所以数列{an-n}(n=1,2,…)是一个以-2为首项,3为公比的等比数列……
……………………………………………………………………………………8分
(Ⅱ)由(Ⅰ)可得an-n=-2?3n-1,
∴an=n-2?3n-1……………………………………………………………………9分
∴a1+a2+a3+…+an=(1-2×1)+(2-2×3)+(3-2×32)+…+(n-2×3n-1)
=(1+2+3+…+n)-(2×1+2×3+2×32+…+2×3n-1) ………………………11分
= .……………………………………………13分
.……………………………………………13分
(19)(本小题满分14分)
解:(Ⅰ)∵曲线y=f (x)在点(0,f (0))处的切线与x轴平行,
∴f (0)=0. ………………………………………………………………………………2分
又f ′ (x)=3x2+2bx+c,则f ′ (0)=c=0.…………………………………………………4分
(Ⅱ)由c=0,方程f (x)-b2x=0可化为x3+bx2-b2x+5=0,
假设存在实数b使得此方程恰有一个实数根,
令g (x)=x3+bx2-b2x+5,则g (x)极大值<0或g (x)极小值>0.
∴g′ (x)=3x2+2bx-b2=(3x-b)(x+b).
令g′ (x)=0,得x1= ,x2=-b.……………………………………………………5分
,x2=-b.……………………………………………………5分
①若b=0,则方程f (x)-b2x=0可化为x3+5=0,此方程恰有一个实根
x=- .………………………………………………………………………………6分
.………………………………………………………………………………6分
②若b>0,则 >-b,列表:
>-b,列表:
x
(?∞,?b)
-b
(-b, )
)

( ,+∞)
,+∞)
g′ (x)
+
0
-
0
+
g (x)
ㄊ
极大值
ㄋ
极小值
ㄊ
∴g (x)极大值=g(-b)=b3+5>0,g (x)极小值=g ( )=-
)=- +5.
+5.
∴- +5>0,解之得0<b<3. ……………………………………………………9分
+5>0,解之得0<b<3. ……………………………………………………9分
③若b<0,则 <-b,列表:
<-b,列表:
x
(?∞, )
)

( ,-b)
,-b)
-b
(-b,+∞)
g′ (x)
+
0
-
0
+
g (x)
ㄊ
极大值
ㄋ
极小值
ㄊ
∴g (x)极大值=g ( )=-
)=- +5>0,g (x)极小值=g(-b)=b3+5.
+5>0,g (x)极小值=g(-b)=b3+5.
∴b3+5>0,解之得b>- .
.
∴- <b<0.
…………………………………………………………………………12分
<b<0.
…………………………………………………………………………12分
综合①②③可得,实数b的取疽范围是(- ,3).…………………………………14分
,3).…………………………………14分
(20)(本小题满分14分)
解:(Ⅰ)f (x)=x2是其定义域上的T函数,………………………………………………2分
证明如下:
对任意实数x1,x2(x1≠x2),
有f ( x1+
x1+ x2)-
x2)- f (x1)-
f (x1)- f(x2)
f(x2)
=( x1+
x1+ x2)2-
x2)2-
 -
-

=- (x1-x2)2<0.
(x1-x2)2<0.
即f ( x1+
x1+ x2)<
x2)< f (x1)+
f (x1)+ f (x2).
f (x2).
∴f(x)=x2是其定义域上的T函数.……………………………………………………4分
(Ⅱ)假设f (x)是R上的T函数,取x1=1,x2=-1,
则有f ( ×1+
×1+ ×(-1))<
×(-1))< f (1)+
f (1)+ f (-1).
f (-1).
∵f (x)是奇函数,
∴f (-1)=-f (1),f (? )=-f(
)=-f( ).
).
∴f( )>
)> f (1).(#)
f (1).(#)
同理,取x1=-1,x2=1,可证f ( )<
)< f (1).
f (1).
与(#)式矛盾.
∴f (x)不是R上的T函数.……………………………………………………………9分
(Ⅲ)对任意0≤n≤m,取x1=m,x2=0,α= ∈[0,1].
∈[0,1].
∵f (x)是R上的C函数,an=f (n),且a0=0,am=
∴an=f (n)=f (αx1+(1-α)x2)≤αf (x1)+(1-α)f
(x2)= ×
×
那么Sf=a1+a2+…+am≤(2×(1+2+…+m)=m2+m.
可证f (x)=2x是C函数,且使得an=2n (n=0,l,2,…,m)都成立,
此时Sf=m2+m.
综上所述,Sf的最大值为m2+m.………………………………………………………14分
说明:其他正确解法按相应步骤给分.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com