练习册

  • 练习册
  • 试题
    (参考数据:) 【查看更多】

     

    题目列表(包括答案和解析)

    据《中国新闻网》10月21日报道，全国很多省市将英语考试作为高考改革的重点，一时间“英语考试该如何改”引起广泛关注．为了解某地区学生和包括老师、家长在内的社会人士对高考英语改革的看法，某媒体在该地区选择了3600人调查（若所选择的在校学生的人数低于被调查人群总数的80%，则认为本次调查“失效”），就“是否取消英语听力”的问题，调查统计的结果如下表：
    态度
    调查人群    		 应该取消 应该保留 无所谓
    在校学生 2100人 120人 y人
    社会人士 600人 x人 z人
    已知在全体样本中随机抽取1人，抽到持“应该保留”态度的人的概率为0.05．
    （Ⅰ）现用分层抽样的方法在所有参与调查的人中抽取360人进行深入访谈，问应在持“无所谓”态度的人中抽取多少人？
    （Ⅱ）已知y≥657，z≥55，求本次调查“失效”的概率．

    查看答案和解析>>

    据《中国新闻网》10月21日报道，全国很多省市将英语考试作为高考改革的重点，一时间“英语考试该如何改”引起广泛关注．为了解某地区学生和包括老师、家长在内的社会人士对高考英语改革的看法，某媒体在该地区选择了3600人调查，就是否“取消英语听力”的问题，调查统计的结果如下表：

     

    应该取消

    应该保留

    无所谓

    在校学生

    2100人

    120人

    y人

    社会人士

    600人

    x人

    z人

    已知在全体样本中随机抽取1人，抽到持“应该保留”态度的人的概率为0.05．

    （Ⅰ）现用分层抽样的方法在所有参与调查的人中抽取360人进行问卷访谈，问应在持“无所谓”态度的人中抽取多少人？

    （Ⅱ）在持“应该保留”态度的人中，用分层抽样的方法抽取6人平均分成两组进行深入交流，求第一组中在校学生人数ξ的分布列和数学期望．

     

    查看答案和解析>>

    据《中国新闻网》10月21日报道，全国很多省市将英语考试作为高考改革的重点，一时间“英语考试该如何改”引起广泛关注．为了解某地区学生和包括老师、家长在内的社会人士对高考英语改革的看法，某媒体在该地区选择了3600人调查（若所选择的在校学生的人数低于被调查人群总数的80%，则认为本次调查“失效”），就“是否取消英语听力”的问题，调查统计的结果如下表：

     

    应该取消

    应该保留

    无所谓

    在校学生

    2100人

    120人

    y人

    社会人士

    600人

    x人

    z人

    已知在全体样本中随机抽取1人，抽到持“应该保留”态度的人的概率为0.05．

    （Ⅰ）现用分层抽样的方法在所有参与调查的人中抽取360人进行深入访谈，问应在持“无所谓”态度的人中抽取多少人？

    （Ⅱ）已知y≥657，z≥55，求本次调查“失效”的概率．

     

    查看答案和解析>>

    （本小题满分12分）某校从参加高一年级期末考试的学生中抽出60名学生，将其某科成绩（是不小于40不大于100的整数）分成六段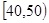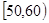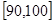，…后画出如下频率分布直方图,根据图形中所给的信息，回答以下问题：

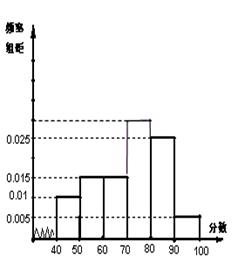
    （1）求第四小组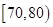的频率.

    （2）求样本的众数.

    (3) 观察频率分布直方图图形的信息，估计这次考试的及格率（60分及以上为及格）和平均分．

     

    查看答案和解析>>

    （本小题满分12分）

    根据公安部最新修订的《机动车驾驶证申领和使用规定》：每位驾驶证申领者必须通过《科目一》（理论科目）、《综合科》（驾驶技能加科目一的部分理论）的考试.已知李先生已通过《科目一》的考试，且《科目一》的成绩不受《综合科》的影响，《综合科》三年内有5次预约考试的机会，一旦某次考试通过，便可领取驾驶证，不再参加以后的考试，否则就一直考到第5次为止.设李先生《综合科》每次参加考试通过的概率依次为0.5，0.6，0.7，0.8，0.9．

    （1）求在三年内李先生参加驾驶证考试次数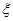的分布列和数学期望；

    （2）求李先生在三年内领到驾驶证的概率.

     

    查看答案和解析>>

      1．2     2．有的素数不是奇数   3．      4．0      5．

      6．   7．  8．[0，2]    9．    10．－3   11．-1 

      12．④    13．     14．①③

    　15．解：（1）因为，所以，

    　　　　即 

    　　　　而  ，所以．故

    　　　　（2）因为 

       　　　　  所以  ．

       　　　 由得   所以  

     　　　　从而 故的取值范围是．

    　16．（1）证明：因为PB^平面ABCD，MA^平面ABCD，

    　　　　　所以PB∥MA．

    　　　　　因PBÌ平面BPC，MA (/平面BPC，

    　　　　　所以MA∥平面BPC．同理DA∥平面BPC，

    　　　　　因为MAÌ平面AMD，ADÌ平面AMD，

    　　　　　MA∩AD＝A，所以平面AMD∥平面BPC．

    　　（2）连接AC，设AC∩BD＝E，取PD中点F，

    　　　　　连接EF，MF．

    　　　　　因ABCD为正方形，所以E为BD中点．

    　　　　　因为F为PD中点，所以EF∥=PB．

    　　　　　因为AM∥=PB，所以AM∥=EF．所以AEFM为平行四边形．所以MF∥AE．

    　　　　　因为PB^平面ABCD，AEÌ平面ABCD，所以PB^AE．所以MF^PB．

    　　　　　因为ABCD为正方形，所以AC^BD．

    　　　　　所以MF^BD．所以MF^平面PBD．又MFÌ平面PMD．

    　　　　　所以平面PMD^平面PBD．

    　　　17．解：（1）  令

      则

      由于，则在内的单调递增区间为和

    （2）依题意， 由周期性 

                     

    （3）函数为单调增函数，且当时，，

      　　　此时有

       　　当时，由于，而，则有，

      　　　　 即，即

       　　而函数的最大值为，且为单调增函数，

           则当时，恒有，

         综上，在内恒有，所以方程在内没有实数解．

    18．解：（1）由题意得:（100-x）? 3000 ?(1+2x%) ≥100×3000，

    　  即x2－50x≤0，解得0≤x≤50，    又∵x＞0   ∴0＜x≤50；                        

         （2）设这100万农民的人均年收入为y元，

       则y=   =

        　 即y=－[x－25(a+1)]2+3000+475(a+1)2     (0<x≤50) 

      （i）当0<25(a+1)≤50，即0＜a≤1，当x=25(a+1)时，y最大；

     （ii）当25(a+1)＞50，即a ＞1，函数y在（0,50]单调递增，∴当x=50时，y取最大值．

    　　     答：在0＜a≤1时，安排25(a+1)万人进入企业工作，在a＞1时安排50万人进入企业

                 工作，才能使这100万人的人均年收入最大．

    　　19．（1）解：由①知：；由③知：，即； ∴ 

      　　  (2 ) 证明：由题设知：；

             　　由知，得，有；

    　　设，则，；

      　  ∴

    　　　即  ∴函数在区间[0,1]上同时适合①②③.

     　　　(3) 证明：若,则由题设知:,且由①知,

       　　　　　　　∴由题设及③知：

    　　　　　　　　,矛盾；

    　　　　　　若,则则由题设知：, 且由①知,

      　　　　　　　∴同理得：

    　　　　　　　　,

    　　　　　　　　　矛盾；故由上述知: ．

    20．解： (1) 由题设知：对定义域中的均成立.

                     ∴.   

           即    ∴对定义域中的均成立.

                      ∴ 即（舍去）或.       ∴ .                           

         (2) 由(1)及题设知：，

                      设，

         ∴当时，  ∴.                            

                  当时，，即.

                   ∴当时，在上是减函数.    

                  同理当时，在上是增函数. 

         (3) 由题设知：函数的定义域为，

                   ∴①当时，有.  由(1)及(2)题设知：在为增函数，由其值域为知（无解）；

       ②当时，有.由(1)及(2)题设知：在为减函数, 由其值域为知得，.

              (4) 由(1)及题设知：

           ，

             则函数的对称轴，∴.

            ∴函数在上单调减.    

       ∴

         是最大实数使得恒有成立，

      

         ∴,即

     


    同步练习册答案