
题目列表(包括答案和解析)
 的零点所在的区间是(2,3);②曲线y=4x-x3在点(-1,-3)处的切线方程是y=x-2;③将函数y=2x+1的图象按向量a=(1,-1)平移后得到函数y=2x+1的图象;④函数y=
的零点所在的区间是(2,3);②曲线y=4x-x3在点(-1,-3)处的切线方程是y=x-2;③将函数y=2x+1的图象按向量a=(1,-1)平移后得到函数y=2x+1的图象;④函数y=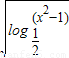 的定义域是(-
的定义域是(-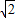 ,-1)∪(1,
,-1)∪(1,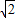 )⑤
)⑤ •
•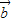 >0是
>0是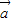 、
、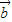 的夹角为锐角的充要条件;以上命题正确的是 .(注:把你认为正确的命题的序号都填上)
的夹角为锐角的充要条件;以上命题正确的是 .(注:把你认为正确的命题的序号都填上)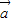 与
与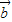 的夹角为α,则cosα<0是
的夹角为α,则cosα<0是 与
与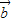 的夹角α为钝角的( )
的夹角α为钝角的( ) 、
、 是两个非零向量,
是两个非零向量,
 >0是
>0是 与
与 的夹角<
的夹角< >为锐角的( )条件
>为锐角的( )条件 、
、 是两个非零向量,
是两个非零向量,
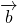 >0是
>0是 与
与 的夹角<
的夹角< >为锐角的______条件
>为锐角的______条件给出下列命题
① 非零向量![]() 、
、![]() 满足|
满足|![]() |=|
|=|![]() |=|
|=|![]() -
-![]() |,则
|,则![]() 与
与![]() +
+![]() 的夹角为30°;
的夹角为30°;
② ![]() ·
·![]() >0是
>0是![]() 、
、![]() 的夹角为锐角的充要条件;
的夹角为锐角的充要条件;
③ 将函数y=|x-1|的图象按向量![]() =(-1,0)平移,得到的图像对应的函数为y=|x|;
=(-1,0)平移,得到的图像对应的函数为y=|x|;
④若(![]() )·(
)·(![]() )=0,则△ABC为等腰三角形
)=0,则△ABC为等腰三角形
以上命题正确的是 。(注:把你认为正确的命题的序号都填上)
1-5 ACADC。 6-10 ACABB 11-12 DA
13.
28 14.  15. -4n+5 ;
15. -4n+5 ; 16. ①③④
16. ①③④
17.(1) ,
, ,即
,即 ,
,
 ,
, ,
, ,
,  ,
,
 ,∴
,∴ . 5分
. 5分

18.解法一:证明:连结OC,

∴ .
----------------------------------------------------------------------------------1分
.
----------------------------------------------------------------------------------1分
 ,
, ,
,
∴ . ------------------------------------------------------2分
. ------------------------------------------------------2分
 在
在 中,
中,
∴ 即
即 ------------------3分
------------------3分

 面
面 . ----------------------------4分
. ----------------------------4分
(II)过O作 ,连结AE,
,连结AE,
 ,
,
∴AE在平面BCD上的射影为OE.
∴ .
.
∴  .
-----------------------------------------7分
.
-----------------------------------------7分
在 中,
中, ,
, ,
, ,
,
∴ .
.
∴二面角A-BC-D的大小为 .
---------------------------------------------------8分
.
---------------------------------------------------8分
(III)解:设点O到平面ACD的距离为
 ,
,
∴ .
.
在 中,
中, ,
,
 .
.
而 ,∴
,∴ .
.
∴点O到平面ACD的距离为 .--------------------------------12分
.--------------------------------12分
解法二:(I)同解法一.
(II)解:以O为原点,如图建立空间直角坐标系,
 则
则 
 ,
,
∴ . ------------6分
. ------------6分
设平面ABC的法向量 ,
,
 ,
, ,
,
由 .
.
设 与
与 夹角为
夹角为 ,则
,则 .
.
∴二面角A-BC-D的大小为 . --------------------8分
. --------------------8分
(III)解:设平面ACD的法向量为 ,又
,又 ,
,
 .
-----------------------------------11分
.
-----------------------------------11分
设 与
与 夹角为
夹角为 ,
,
则  - 设O 到平面ACD的距离为h,
- 设O 到平面ACD的距离为h,
∵ ,∴O到平面ACD的距离为
,∴O到平面ACD的距离为 . ---------------------12分
. ---------------------12分
19.(Ⅰ)解:设“从甲盒内取出的2个球均为黑球”为事件 ,“从乙盒内取出的2个球均为黑球”为事件
,“从乙盒内取出的2个球均为黑球”为事件 .由于事件
.由于事件 相互独立,且
相互独立,且 ,
, .
.
故取出的4个球均为黑球的概率为 .…….6分
.…….6分
(Ⅱ)解:设“从甲盒内取出的2个球均为黑球;从乙盒内取出的2个球中,1个是红球,1个是黑球”为事件 ,“从甲盒内取出的2个球中,1个是红球,1个是黑球;从乙盒内取出的2个球均为黑球”为事件
,“从甲盒内取出的2个球中,1个是红球,1个是黑球;从乙盒内取出的2个球均为黑球”为事件 .由于事件
.由于事件 互斥,
互斥,
且 ,
, .
.
故取出的4个球中恰有1个红球的概率为 ...12分
...12分
20. 解:(Ⅰ)由已知,当 时,
时, ……………… 2分
……………… 2分
由 ,得
,得 ,∴p=
,∴p= …………….4分
…………….4分
∴ .……………… 6分
.……………… 6分
(Ⅱ)由(1)得, . ……………… 7分
. ……………… 7分
 2 ;
①
2 ;
①
 . ② ………9分
. ② ………9分
②-①得,
= =
= . ………………12分
. ………………12分
21.解(I)

(II)

若 时,
时, 是减函数,则
是减函数,则 恒成立,得
恒成立,得

22.解(I)设

(3分)
(Ⅱ)(1)当直线 的斜率不存在时,方程为
的斜率不存在时,方程为

 …………(4分)
…………(4分)
(2)当直线 的斜率存在时,设直线的方程为
的斜率存在时,设直线的方程为 ,
,
设 ,
,
 ,得
,得
 …………(6分)
…………(6分)


 …………………8分
…………………8分
………………….9分

注意也可用 ..........12分
..........12分
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com