
题目列表(包括答案和解析)
| 1 | 12 |
把下列各式因式分解:(本大题共2小题,每题4分,计8分)
① ②
②
(本小题满分12分)
已知二次函数图象的顶点坐标为M(1,0),直线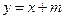 与该二次函数的图象交于A,B两点,其中A点的坐标为(3,4),B点在
与该二次函数的图象交于A,B两点,其中A点的坐标为(3,4),B点在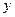 轴上.
轴上.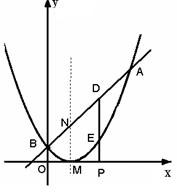
【小题1】(1)求m的值及这个二次函数的解析式;
【小题2】(2)若P(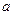 ,0) 是
,0) 是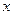 轴上的一个动点,过P作
轴上的一个动点,过P作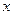 轴的垂线分别与直线AB和二次函数的图象交于D、E两点.
轴的垂线分别与直线AB和二次函数的图象交于D、E两点.
①当0<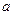 < 3时,求线段DE的最大值;
< 3时,求线段DE的最大值;
②若直线AB与抛物线的对称轴交点为N,
问是否存在一点P,使以M、N、D、E
为顶点的四边形是平行四边形?若存在,
请求出此时P点的坐标;若不存在,请
说明理由.
| 湘 莲 品 种 | A | B | C |
| 每辆汽车运载量(吨) | 12 | 10 | 8 |
| 每吨湘莲获利(万元) | 3 | 4 | 2 |
(本大题12分)某镇组织10辆汽车装运完A、B、C三种不同品质的湘莲共100吨到外地销售,按计划10辆汽车都要装满,且每辆汽车只能装同一种湘莲,根据下表提供的信息,解答以下问题:
(1)设装运A种湘莲的车辆数为x,装运B种湘莲的车辆数为y,求y与x之间的函数关系式;
(2)如果装运每种湘莲的车辆数都不少于2辆,那么车辆的安排方案有几种?并写出每种安排方案;
(3)在(2)的方案中,若要使此次销售获利最大,应采用哪种安排方案?并求出最大利润的值.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com