我市某地为了贯彻落实“森林重庆”,深入开展“绿化长江---重庆行动”.现决定对该地区培育种植树苗的农民实行政府补贴,规定每种植一亩树苗一次性补贴农民若干元,随着补贴数额的不断增大,生产规模也不断增加,但每亩树苗的收益会相应降低.经调查,种植亩数y(亩)、每亩树苗的收益z(元)与补贴数额x(元)之间的一次函数关系如下表:
| x(元) |
0 |
100 |
200 |
300 |
… |
| y(亩) |
800 |
1600 |
2400 |
3200 |
… |
| z(元) |
3000 |
2700 |
2400 |
2100 |
… |
(1)分别求出政府补贴政策实施后种植亩数y、每亩树苗的收益z与政府补贴数额x之间的函数关系式:
(2)要使该地区种植树苗的总收益w(元)最大,政府应将每亩补贴数额x定为多少?并求出总收益w的最大值和此时种植的亩数;(总收益=种植亩数×每亩树苗的收益)
(3)在取得最大收益的情况下,经市场调查,培育种植水果类树苗经济效益更好.今年该地区决定用种植树苗总面积m%的土地种植水果类树苗,因环境和经济等因素的制约,种植水果类树苗的面积不超过300亩.经测算,种植水果类树苗需用的支架、塑料膜等材料每亩费用为2700元,此外还需购置喷灌设备,这项费用(元)与种植水果类树苗面积(亩)的平方成正比例,比例系数9.预计今年种植水果类树苗后的这部分土地的收益比没种前的收益每亩增加了7500元,这样,该地区今年因种植水果类树苗而增加的收益(扣除材料费和设备费后)共570000元,求m的值.(结果精确到个位,参考数据:
≈2.648,
≈3.316).

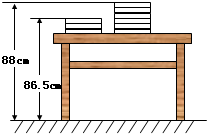 新学期,两摞规格相同的数学课本整齐的叠放在讲台上,请根据图中所给出的数据信息,解答下列问题:
新学期,两摞规格相同的数学课本整齐的叠放在讲台上,请根据图中所给出的数据信息,解答下列问题: 新学期,两摞规格相同的数学课本整齐的叠放在讲台上,请根据图中所给出的数据信息,解答下列问题:
新学期,两摞规格相同的数学课本整齐的叠放在讲台上,请根据图中所给出的数据信息,解答下列问题: