
题目列表(包括答案和解析)
(本小题满分10分)
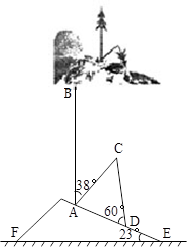 2011年3月11日13时46分日本发生了9.0级大地震,伴随着就是海啸。山坡上有一棵与水平面垂直的大树,海啸过后,大树被刮倾斜后折断倒在山坡上,树的顶部恰好接触到坡面(如图所示)。
2011年3月11日13时46分日本发生了9.0级大地震,伴随着就是海啸。山坡上有一棵与水平面垂直的大树,海啸过后,大树被刮倾斜后折断倒在山坡上,树的顶部恰好接触到坡面(如图所示)。
已知山坡的坡角∠AEF=23°,量得树干的倾斜角为
∠BAC=38°,大树被折断部分和坡面所成的角∠ADC=60°,AD=4m。
(1)求∠DAC的度数;
(2)求这棵大树折点C到坡面AE的距离?
 (结果精确到个位,参考数据:
(结果精确到个位,参考数据:,
,
).
(本小题满分10分)
 2011年3月11日13时46分日本发生了9.0级大地震,伴随着就是海啸。山坡上有一棵与水平面垂直的大树,海啸过后,大树被刮倾斜后折断倒在山坡上,树的顶部恰好接触到坡面(如图所示)。
2011年3月11日13时46分日本发生了9.0级大地震,伴随着就是海啸。山坡上有一棵与水平面垂直的大树,海啸过后,大树被刮倾斜后折断倒在山坡上,树的顶部恰好接触到坡面(如图所示)。
已知山坡的坡角∠AEF=23°,量得树干的倾斜角为
∠BAC=38°,大树被折断部分和坡面所成的角∠ADC=60°,AD=4m。
(1)求∠DAC的度数;
(2)求这棵大树折点C到坡面AE的距离?
 (结果精确到个位,参考数据:
(结果精确到个位,参考数据: ,
, ,
, ).
).
【改编】(本小题满分10分)
2011年3月11日13时46分日本发生了9.0级大地震,伴随着就是海啸。山坡上有一棵与水平面垂直的大树,海啸过后,大树 被刮倾斜后折断倒在山坡上,树的顶部恰好接触到坡面(如图所示)。已知山坡的坡角∠AEF=23°,量得树干的倾斜角为∠BAC=38°,大树被折断部分和坡面所成的角∠ADC=60°,AD=4m。
被刮倾斜后折断倒在山坡上,树的顶部恰好接触到坡面(如图所示)。已知山坡的坡角∠AEF=23°,量得树干的倾斜角为∠BAC=38°,大树被折断部分和坡面所成的角∠ADC=60°,AD=4m。
(1)求∠DAC的度数;
(2)求这棵大树折点C到坡面AE的距离?
|
 ,
, ,
, ).
).
| 13 |
| 13 |
| 13 |

(11·贺州)(本题满分10分).
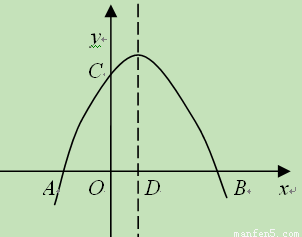
如图,在平面直角坐标系中,抛物线与x轴交于A、B两点(A在B的左侧),与y轴交于
(1)求抛物线的函数表达式;
(2)设抛物线的对称轴与轴交于点D,试在对称轴上找出点P,使△CDP为等腰三角形,
请直接写出满足条件的所有点P的坐标.
(3)若点E是线段AB上的一个动点(与A、B不重合),分别连接AC、BC,过点E作EF
∥AC交线段BC于点F,连接CE,记△CEF的面积为S,S是否存在最大值?若存在,求
出S的最大值及此时E点的坐标;若不存在,请说明理由.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com