
题目列表(包括答案和解析)
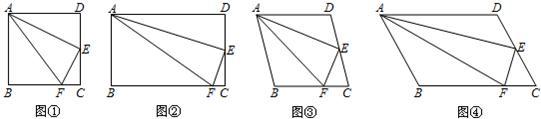
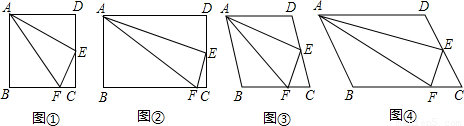

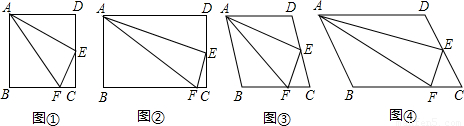
如图,小明在研究正方形ABCD的有关问题时,得出:“在正方形ABCD中,如果点E是CD的中点,点F是BC边上的一点,且∠FAE =∠EAD,那么EF⊥AE”.他又将“正方形”改为“矩形”、“菱形”和“任意平行四边形”(如图2、图3、图4),其他条件不变,发现仍然有“EF⊥AE”的结论.
你同意小明的观点吗?若同意,请结合图1-4加以证明;若不同意,请说明理由.

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com