
题目列表(包括答案和解析)
![]() 分别等于1和
分别等于1和![]() 时,代数式
时,代数式![]() 相应的两个的值( )
相应的两个的值( )
A.相等 B.同号 C.互为相反数 D.互为倒数
如图,在直角坐标系中,![]() 是原点,
是原点,![]() 三点的坐标分别
三点的坐标分别![]() ,四边形
,四边形![]() 是梯形,点
是梯形,点![]() 同时从原点出发,分别作匀速运动,其中点
同时从原点出发,分别作匀速运动,其中点![]() 沿
沿![]() 向终点
向终点![]() 运动,速度为每秒
运动,速度为每秒![]() 个单位,点
个单位,点![]() 沿
沿![]() 向终点
向终点![]() 运动,当这两点有一点到达自己的终点时,另一点也停止运动.
运动,当这两点有一点到达自己的终点时,另一点也停止运动.
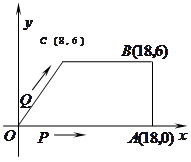
(1)求直线![]() 的解析式.
的解析式.
(2)设从出发起,运动了![]() 秒.如果点
秒.如果点![]() 的速度为每秒
的速度为每秒![]() 个单位,试写出点
个单位,试写出点![]() 的坐标,并写出此时
的坐标,并写出此时![]() 的取值范围.
的取值范围.
(3)设从出发起,运动了![]() 秒.当
秒.当![]() ,
,![]() 两点运动的路程之和恰好等于梯形
两点运动的路程之和恰好等于梯形![]() 的周长的一半,这时,直线
的周长的一半,这时,直线![]() 能否把梯形的面积也分成相等的两部分,如有可能,请求出
能否把梯形的面积也分成相等的两部分,如有可能,请求出![]() 的值;如不可能,请说明理由.
的值;如不可能,请说明理由.
【解析】(1)根据待定系数法就可以求出直线OC的解析式(2)本题应分Q在OC上,和在CB上两种情况进行讨论.即0≤t≤5和5<t≤10两种情况(3)P、Q两点运动的路程之和可以用t表示出来,梯形OABC的周长就可以求得.当P、Q两点运动的路程之和恰好等于梯形OABC的周长的一半,就可以得到一个关于t的方程,可以解出t的值.梯形OABC的面积可以求出,梯形OCQP的面积可以用t表示出来.把t代入可以进行检验
如图,在直角坐标系中,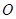 是原点,
是原点,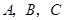 三点的坐标分别
三点的坐标分别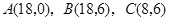 ,四边形
,四边形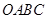 是梯形,点
是梯形,点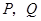 同时从原点出发,分别作匀速运动,其中点
同时从原点出发,分别作匀速运动,其中点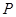 沿
沿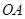 向终点
向终点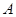 运动,速度为每秒
运动,速度为每秒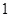 个单位,点
个单位,点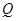 沿
沿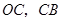 向终点
向终点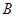 运动,当这两点有一点到达自己的终点时,另一点也停止运动.
运动,当这两点有一点到达自己的终点时,另一点也停止运动.

(1)求直线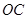 的解析式.
的解析式.
(2)设从出发起,运动了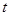 秒.如果点
秒.如果点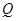 的速度为每秒
的速度为每秒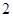 个单位,试写出点
个单位,试写出点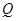 的坐标,并写出此时
的坐标,并写出此时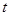 的取值范围.
的取值范围.
(3)设从出发起,运动了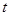 秒.当
秒.当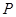 ,
,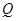 两点运动的路程之和恰好等于梯形
两点运动的路程之和恰好等于梯形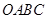 的周长的一半,这时,直线
的周长的一半,这时,直线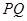 能否把梯形的面积也分成相等的两部分,如有可能,请求出
能否把梯形的面积也分成相等的两部分,如有可能,请求出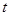 的值;如不可能,请说明理由.
的值;如不可能,请说明理由.
【解析】(1)根据待定系数法就可以求出直线OC的解析式(2)本题应分Q在OC上,和在CB上两种情况进行讨论.即0≤t≤5和5<t≤10两种情况(3)P、Q两点运动的路程之和可以用t表示出来,梯形OABC的周长就可以求得.当P、Q两点运动的路程之和恰好等于梯形OABC的周长的一半,就可以得到一个关于t的方程,可以解出t的值.梯形OABC的面积可以求出,梯形OCQP的面积可以用t表示出来.把t代入可以进行检验
| 3 | 4 |
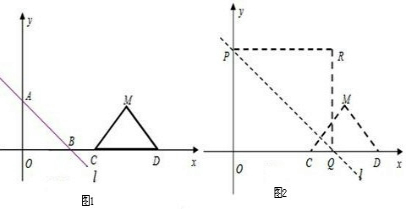
 x+3分别交x轴、y轴于B、A两点,等腰直角△CDM斜边落在x轴上,且CD=6,如图1所示.若直线l以每秒3个单位向上作匀速平移运动,同时点C从(6,0)开始以每秒2个单位的速度向右作匀速平移运动,如图2所示,设移动后直线l运动后分别交x轴、y轴于Q、P两点,以OP、OQ为边作如图矩形OPRQ.设运动时间为t秒.
x+3分别交x轴、y轴于B、A两点,等腰直角△CDM斜边落在x轴上,且CD=6,如图1所示.若直线l以每秒3个单位向上作匀速平移运动,同时点C从(6,0)开始以每秒2个单位的速度向右作匀速平移运动,如图2所示,设移动后直线l运动后分别交x轴、y轴于Q、P两点,以OP、OQ为边作如图矩形OPRQ.设运动时间为t秒.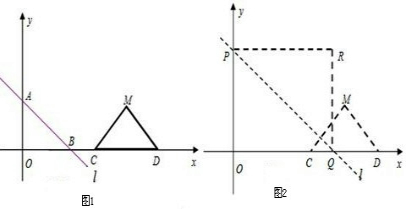
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com