
题目列表(包括答案和解析)

 探索与应用
探索与应用| a | 2 | 0 | -2 | … | ||||
| b | -3 |
|
1 | … | ||||
| a2-b2 | -5 -5 |
-
-
|
3 3 |
… | ||||
| (a+b)(a-b) | -5 -5 |
-
-
|
3 3 |
… |
探索与应用
【列 式】
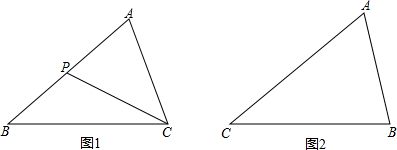
在边长为 的正方形中挖去一个边长为
的正方形中挖去一个边长为 的小正方形(
的小正方形( >
> )(如图甲),把余下的部分剪拼成一个长方形(如图乙),
)(如图甲),把余下的部分剪拼成一个长方形(如图乙),
试用 、
、 列式:
列式:
图甲中阴影部分的面积为 ,
图乙中阴影部分的面积为 。
【填 表】
根据表格所给的a、b的值,计算 与
与 的值,并将计算结果填入表中
的值,并将计算结果填入表中
| a | 2 | 0 | -2 | … |
| b | -3 | 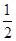 | 1 | … |
 | | | | … |
 | | | | … |

 (填“>”,“=”或“<”)
(填“>”,“=”或“<”)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com