某批发商欲将一批海产品由A地运往B地，汽车货运公司和铁路货运公司均开办了海产品运输业务。已知运输路程为120千米，汽车和火车的速度分别为60千米／时和100千米／时，两货运公司的收费项目和收费标准如下表所示：

运输 工具	运输费单价 （元／吨·千米）	冷藏费单价 （元／吨·小时）	过路费（元）	装卸及管理费（元）
汽车	2	5	200	0
火车	1.8	5	0	1600

注：“元／吨·千米”表示每吨货物每千米的运费：“元／吨·小时”表示每吨货物每小时的冷藏费。

（1）设该批发商待运的海产品有（吨），汽车货运公司和铁路货运公司所要收取的费用分别为（元）和（元），试求出、与的函数关系式；

（2）若该批发商待运的海产品不少于30吨，为节省运费，他应该选择哪个货运公司承担运输业务?

市“健益”超市购进一批20元／千克的绿色食品。如果以30元／千克销售。那么每天可售出400千克，由销售经验知，每天销售售量y(千克)与销售单价(元) (≥30)存在如下图所示的一次函数关系。

(1)试求出y与的函数关系式;

(2)设“健益”超市销售该绿色食品每天获得利润P元，当销售单价为何值时，每天可获得最大利润?最大利润是多少?

在Rt△ABC中，∠BAC=90°，AB=AC=4cm，实验操作：把一等腰直角三角尺45°角的顶点（记为点D），放在BC边上滑动（不与B，C重合），让该角的一边始终过点A，另一边交AC于点E，选取运动过程中的两个瞬间，用量角器分别测出∠BDA与∠CED的大小，并填入下表：

	∠BDA	∠CED
第一次测量结果
第二次测量结果

探索：（1）观察实验结果，猜想∠BDA与∠CED的大小有何关系？并证明你的结论；
（2）设BD=x，AE=y，试求出y关于x的函数关系式，并写出自变量x的取值范围；
（3）当点D在BC边上滑动时，△ADE能否成为等腰三角形？若能，求出点D的位置；若不能，请说明理由．（图1供实验操作用，图2备用）

如图所示，在直角坐标系xOy中，正方形ABCD的四个顶点坐标为A（0，6），B（2，4），C（4，6），D（2，8）．动点M在正方形ABCD的边上，从点A出发沿A→B→C→D向终点D匀速运动，速度为每秒

2

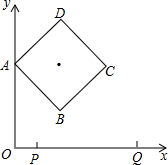个长度单位，同时动点N以每秒1个单位长度的速度从点P（1，0）出发沿x轴向终点Q（7，0）匀速运动，设两点运动的时间为t秒．
（1）求线段AB的解析式，并指出x的取值范围；
（2）求经过A、B、C三点的抛物线y=ax²+bx+c的解析式；
（3）当点M在边AB上运动时，△OMN的面积为S，试求出S关于t的函数关系式及t的取值范围，并指出当t为何值时，S有最大值．
（4）两动点M、N在运动过程中，OM与MN能否相等？若能，直接写出（不要解答过程）所有符合条件的t的值；若不能，请说明理由．