
题目列表(包括答案和解析)
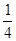 x2+bx+c过B、C两点
x2+bx+c过B、C两点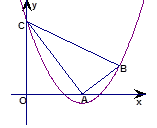
(本题10分)如图,已知△ABC中,∠A=90°,AC=10,AB=5,点A、C分别在x轴和y轴上,且C(0,8),抛物线y=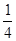 x2+bx+c过B、C两点
x2+bx+c过B、C两点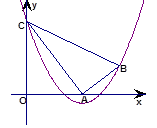
【小题1】⑴求抛物线解析式.
【小题2】⑵如果将△ABC沿CA翻折,设点B的落点为点M,现平移抛物线,使它的顶点为M,求出平移后的抛物线解析式,并写出平移的方法.
(本题10分)如图,在Rt△ABC中,∠B=90°,AB=1,BC=![]() ,以点C为圆心,CB为半径的弧交CA于点D;以点A为圆心,AD为半径的弧交AB于点E.
,以点C为圆心,CB为半径的弧交CA于点D;以点A为圆心,AD为半径的弧交AB于点E.
(1)求AE的长度;
(2)分别以点A、E为圆心,AB长为半径画弧,两弧交于点F(F与C在AB两侧),连接AF、EF,设EF交弧DE所在的圆于点G,连接AG,
① 求证:△AEG∽△FEA;
② 试猜想∠EAG的大小,并说明理由.
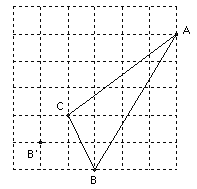
(本题10分)在正方形网格中,每个小正方形的边长均为1个单位长度,△ABC的三个顶点的位置如图所示.

(1)过点B′画出平移后的△A′B′C′,使A′和A、B′和B、C′和C分别对应;
(2)若连接AA′、BB′、CC′,则这三条线段之间的关系是______ ,仔细观察,图中互相平行的线段共有 对;
(3)求△A′B′C′的面积.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com