
题目列表(包括答案和解析)
 的黄金分割点.某研究小组在进行课题学习时,由黄金分割点联想到“黄金分割线”,类似地给出“黄金分割线”的定义:直线
的黄金分割点.某研究小组在进行课题学习时,由黄金分割点联想到“黄金分割线”,类似地给出“黄金分割线”的定义:直线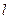 将一个面积为S的图形分成两部分,这两部分的面积分别为S1: S2,如果S : S1= S1: S2,,那么称直线
将一个面积为S的图形分成两部分,这两部分的面积分别为S1: S2,如果S : S1= S1: S2,,那么称直线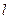 为该图形的黄金分割线.
为该图形的黄金分割线. ,交 AC于点F,连接EF(如图3),则直线EF是△ABC的黄金分割线.请说明理由.
,交 AC于点F,连接EF(如图3),则直线EF是△ABC的黄金分割线.请说明理由. ABCD的边AB的黄金分割点,过点E作
ABCD的边AB的黄金分割点,过点E作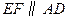 ,交DC于点F,显然直线EF是
,交DC于点F,显然直线EF是 ABCD的黄金分割线.请你再画一条
ABCD的黄金分割线.请你再画一条 ABCD的黄金分割线,使它不经过
ABCD的黄金分割线,使它不经过 ABCD各边黄金分割点(保留必要的辅助线).
ABCD各边黄金分割点(保留必要的辅助线).
(本小题满分10分)
如图14①至图14④中,两平行线AB、CD音的距离均为6,点M为AB上一定点.
思考:如图14①中,圆心为O的半圆形纸片在AB、CD之间(包括AB、CD),其直径MN在AB上,MN=8,点P为半圆上一点,设∠MOP=α,当α=________度时,点P到CD的距离最小,最小值为____________.
探究一在图14①的基础上,以点M为旋转中心,在AB、CD之间顺时针旋转该半圆形纸片,直到不能再转动为止.如图14②,得到最大旋转角∠BMO=_______度,此时点N到CD的距离是______________.
探究二将图14①中的扇形纸片NOP按下面对α的要求剪掉,使扇形纸片MOP绕点M在AB、CD之间顺时针旋转.
⑴如图14③,当α=60°时,求在旋转过程中,点P到CD的最小距离,并请指出旋转角∠BMO的最大值:
⑵如图14④,在扇形纸片MOP旋转过程中,要保证点P能落在直线CD上,请确定α的取值范围.
(参考数据:sin49°=![]() ,cos41°=
,cos41°=![]() ,tan37°=
,tan37°=![]() )
)
(本小题满分10分)如图,有长为30m的篱笆,一面利用墙(墙的最大可用长度为10m),围成中间隔有一道篱笆(平行于 )的矩形花圃,设花圃一边
)的矩形花圃,设花圃一边 的长为
的长为 m,面积为
m,面积为 .
.
(1)求 与
与 的函数关系式;
的函数关系式;
(2)如果要围成面积为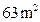 的花圃,
的花圃, 的长是多少?
的长是多少?
(3)能围成面积比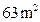 更大的花圃吗?如果能,请求出最大面积;如果不能,请说明理由.
更大的花圃吗?如果能,请求出最大面积;如果不能,请说明理由.
(本小题满分10分)
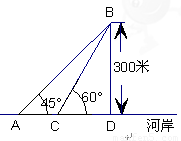
如图,某地海岸线可以近似地看作一条直线,两救生员在岸边A处巡查,发现在海中B处有人求救,救生员甲与乙都没有直接从A处游向B处,甲是沿岸边A处跑到离B最近的D处,然后游向B处;乙是沿岸边A处跑到点C处然后游向B处,若两救生员在岸边的行进速度都为6米∕秒,在海水中的行进速度都为2米∕秒,试分析救生员的选择是否正确?谁先到达点B处?(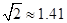 ,
,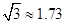 )
)
(本小题满分10分)
如图14①至图14④中,两平行线AB、CD音的距离均为6,点M为AB上一定点.
思考:如图14①中,圆心为O的半圆形纸片在AB、CD之间(包括AB、CD),其直径MN在AB上,MN=8,点P为半圆上一点,设∠MOP=α,当α=________度时,点P到CD的距离最小,最小值为____________.
探究一在图14①的基础上,以点M为旋转中心,在AB、CD之间顺时针旋转该半圆形纸片,直到不能再转动为止.如图14②,得到最大旋转角∠BMO=_______度,此时点N到CD的距离是______________.
探究二将图14①中的扇形纸片NOP按下面对α的要求剪掉,使扇形纸片MOP绕点M在AB、CD之间顺时针旋转.
⑴如图14③,当α=60°时,求在旋转过程中,点P到CD的最小距离,并请指出旋转角∠BMO的最大值:
⑵如图14④,在扇形纸片MOP旋转过程中,要保证点P能落在直线CD上,请确定α的取值范围.
(参考数据:sin49°= ,cos41°=
,cos41°= ,tan37°=
,tan37°= )
)

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com