
题目列表(包括答案和解析)
 x上有一点A,AD⊥x轴于D,且AD=3,C是x轴上的一点,CA ⊥AO, 长度等于OD的线段EF在x轴上沿OC方向以1/s的速度向点C运动(运动前EF和OD重合,当F点与C重合时停止运动,包括起点、终点),过E,F分别作OC的垂线交直角边于点P、点Q,连结线段PD,QD,PQ,PQ交线段AD于点M,若设EF运动的时间为t(s),
x上有一点A,AD⊥x轴于D,且AD=3,C是x轴上的一点,CA ⊥AO, 长度等于OD的线段EF在x轴上沿OC方向以1/s的速度向点C运动(运动前EF和OD重合,当F点与C重合时停止运动,包括起点、终点),过E,F分别作OC的垂线交直角边于点P、点Q,连结线段PD,QD,PQ,PQ交线段AD于点M,若设EF运动的时间为t(s), 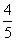 秒时,线段AM= ______;
秒时,线段AM= ______; 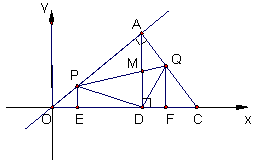
已知:以原点O为圆心,5为半径的半圆与y轴交于A、G两点,AB与半圆相切于点A,点B的坐标为(3, )。(如图1
)。(如图1 )过半圆上的点C
)过半圆上的点C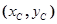 作y轴的垂线,垂足为D.Rt△DOC的面积为
作y轴的垂线,垂足为D.Rt△DOC的面积为 。
。
(1)求点C的坐标;
(2)①命题“如图2,以y轴为对称轴的等腰梯形MNPQ与M1N1P1Q1的上底和下底都分别在同一条直线上,NP∥MQ,PQ∥P1Q1,且NP>MQ.设抛物线y=a0x2+h0过点P、Q,抛物线y=a1x2+h1过点P1、Q1,则h0>h1”是真命题.请你以Q(3,5)、P(4,3)和Q1(p,5)、P1(p+1,3)为例进行验证;
②当图1中的线段BC在第一象限时,作线段BC关于y轴对称的线段FE,连接BF、CE,点T是线段BF上的动点(如图3);设K是过T、B、C三点的抛物线y=ax2+bx+c的顶点,求K的纵坐标yK的取值范围.
如图,抛物线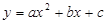 与
与 轴交于A、B两点(点A在点B左侧),与y轴交于点C,且当
轴交于A、B两点(点A在点B左侧),与y轴交于点C,且当 =O和
=O和 =4时,y的值相等。直线y=4x-16与这条抛物线相交于两点,其中一点的横坐标是3,另一点是这条抛物线的顶点M。
=4时,y的值相等。直线y=4x-16与这条抛物线相交于两点,其中一点的横坐标是3,另一点是这条抛物线的顶点M。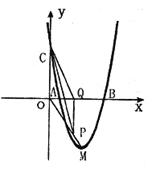
(1)求这条抛物线的解析式;
(2)P为线段OM上一点,过点P作PQ⊥ 轴于点Q。若点P在线段OM上运动(点P不与点O重合,但可以与点M重合),设OQ的长为t,四边形PQCO的面积为S,求S与t之间的函数关系式及自变量t的取值范围;
轴于点Q。若点P在线段OM上运动(点P不与点O重合,但可以与点M重合),设OQ的长为t,四边形PQCO的面积为S,求S与t之间的函数关系式及自变量t的取值范围;
(3)随着点P的运动,四边形PQCO的面积S有最大值吗?如果S有最大值,请求出S的最大值并指出点Q的具体位置和四边形PQCO的特殊形状;如果S没有最大值,请简要说明理由;
(4)随着点P的运动,是否存在t的某个值,能满足PO=OC?如果存在,请求出t的值。
如图,抛物线 与
与 轴交于A、B两点(点A在点B左侧),与y轴交于点C,且当
轴交于A、B两点(点A在点B左侧),与y轴交于点C,且当 =O和
=O和 =4时,y的值相等。直线y=4x-16与这条抛物线相交于两点,其中一点的横坐标是3,另一点是这条抛物线的顶点M。
=4时,y的值相等。直线y=4x-16与这条抛物线相交于两点,其中一点的横坐标是3,另一点是这条抛物线的顶点M。

(1)求这条抛物线的解析式;
(2)P为线段OM上一点,过点P作PQ⊥ 轴于点Q。若点P在线段OM上运动(点P不与点O重合,但可以与点M重合),设OQ的长为t,四边形PQCO的面积为S,求S与t之间的函数关系式及自变量t的取值范围;
轴于点Q。若点P在线段OM上运动(点P不与点O重合,但可以与点M重合),设OQ的长为t,四边形PQCO的面积为S,求S与t之间的函数关系式及自变量t的取值范围;
(3)随着点P的运动,四边形PQCO的面积S有最大值吗?如果S有最大值,请求出S的最大值并指出点Q的具体位置和四边形PQCO的特殊形状;如果S没有最大值,请简要说明理由;
(4)随着点P的运动,是否存在t的某个值,能满足PO=OC?如果存在,请求出t的值。
 与
与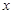 轴交于A、B两点(点A在点B左侧),与y轴交于点C,且当
轴交于A、B两点(点A在点B左侧),与y轴交于点C,且当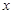 =O和
=O和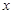 =4时,y的值相等。直线y=4x-16与这条抛物线相交于两点,其中一点的横坐标是3,另一点是这条抛物线的顶点M。
=4时,y的值相等。直线y=4x-16与这条抛物线相交于两点,其中一点的横坐标是3,另一点是这条抛物线的顶点M。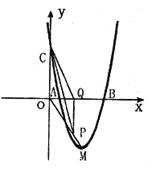
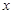 轴于点Q。若点P在线段OM上运动(点P不与点O重合,但可以与点M重合),设OQ的长为t,四边形PQCO的面积为S,求S与t之间的函数关系式及自变量t的取值范围;
轴于点Q。若点P在线段OM上运动(点P不与点O重合,但可以与点M重合),设OQ的长为t,四边形PQCO的面积为S,求S与t之间的函数关系式及自变量t的取值范围;湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com