
题目列表(包括答案和解析)
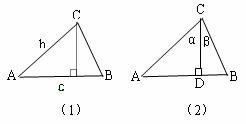
如下图(1),由直角三角形边角关系,可将三角形面积公式变形,
得 ![]() =
=![]() bc?sin∠A. ①
bc?sin∠A. ①
即三角形的面积等于两边之长与夹角正弦之积的一半.
如下图(2),在ABC中,CD⊥AB于D,∠ACD=α, ∠DCB=β.
∵ ![]() , 由公式①,得
, 由公式①,得
![]() AC?BC?sin(α+β)=
AC?BC?sin(α+β)= ![]() AC?CD?sinα+
AC?CD?sinα+![]() BC?CD?sinβ,
BC?CD?sinβ,
即 AC?BC?sin(α+β)= AC?CD?sinα+BC?CD?sinβ. ②
你能利用直角三角形边角关系,消去②中的AC、BC、CD吗?不能,说明理由;能,写出解决过程.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com