练习册

  • 练习册
  • 试题
    问题:如图1.在菱形和菱形中.点在同一条直线上.是线段的中点.连结．若.探究与的位置关系及的值． 【查看更多】

     

    题目列表(包括答案和解析)

    如图，在平面直角坐标系中，点A（3，0），点B（0，3
    		3
    ），连接AB，动点P从A点开始沿折线AO-OB-BA运动，点P在AO、OB、BA上运动的速度分别为1，
    		3
    ，2（长度单位/秒）；同时直线l从x轴的位置开始以
    		3
    3
    （长度单位/秒）的速度向上平行移动，且分别与OB、AB交于E、F两点，设动点P与动直线l同时出发，运动时间为t秒，当点P沿折线AO-OB-BA运动一周时，直线l和动点P同时停止运动．
    请解答下列问题：
    （1）过A、B两点的直线表达式是
    y=-
    		3
    x+3
    		3
    y=-
    		3
    x+3
    		3
    ．
    （2）当t=4时，点P坐标为
    （0，
    		3
    ）
    （0，
    		3
    ）
    ，当t=
    9
    2
    9
    2
    时，点P与点E重合；
    （3）作点P关于直线l的对称点P′，在运动过程中，若形成的四边形PEP′F为菱形，则t的值是多少？
    （4）当t=2时，是否存在点Q，使△FEQ∽△BEP？若存在，直接写出点Q的坐标；若不存在，请说明理由．

    查看答案和解析>>

    27、如图①，小明在研究正方形ABCD的有关问题时，得出：“在正方形ABCD中，如果点E是CD的中点，点F是BC边上的一点，且∠FAE=∠EAD，那么EF⊥AE”．他又将“正方形”改为“矩形”、“菱形”和“任意平行四边形”（如图②、图③、图④），其它条件不变，发现仍然有“EF⊥AE”结论．
    你同意小明的观点吗？同意，请结合图④加以证明；若不同意，请说明理由．

    查看答案和解析>>

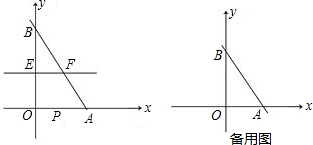
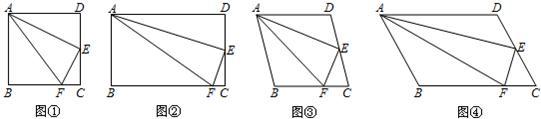
    如图，小明在研究正方形ABCD的有关问题时，得出：“在正方形ABCD中，如果点E是CD的中点，点F是BC边上的一点，且∠FAE =∠EAD，那么EF⊥AE”．他又将“正方形”改为“矩形”、“菱形”和“任意平行四边形”(如图2、图3、图4)，其他条件不变，发现仍然有“EF⊥AE”的结论．

    你同意小明的观点吗？若同意，请结合图1－4加以证明；若不同意，请说明理由．

    查看答案和解析>>

    如图，把含有30°角的三角板ABO置入平面直角坐标系中，A，B两点坐标分别为（3，0）和(0，3）.动点P从A点开始沿折线AO-OB-BA运动，点P在AO，OB，BA上运动的面四民﹒数学兴趣小组对捐款情况进行了抽样调查，速度分别为1，，2 (长度单位/秒)﹒一直尺的上边缘l从x轴的位置开始以 (长度单位/秒)的速度向上平行移动（即移动过程中保持l∥x轴），且分别与OB，AB交于E，F两点﹒设动点P与动直线l同时出发，运动时间为t秒，当点P沿折线AO-OB-BA运动一周时，直线l和动点P同时停止运动．
    请解答下列问题：
    小题1:过A，B两点的直线解析式是      ▲       
    小题2:当t﹦4时，点P的坐标为   ▲    ；当t ﹦   ▲    ，点P与点E重合；
    小题3:① 作点P关于直线EF的对称点P′. 在运动过程中，若形成的四边形PEP′F为菱形，则t的值是多少？
    ② 当t﹦2时，是否存在着点Q，使得△FEQ ∽△BEP ?若存在, 求出点Q的坐标；若不存在，请说明理由．

    查看答案和解析>>

    问题：如图（12），在菱形和菱形中，点在同一条直线上，是线段 的中点，连结．探究与的位置关系及的值．小聪同学的思路是：延长交于点，构造全等三角形，经过推理使问题得到解决．

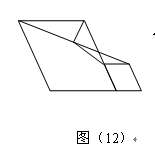
    请你参考小聪同学的思路，探究并解决下列问题：

    1.若图（12）中，写出线段与的位置关系及的值，并说明理由；

    2.将图（12）中的菱形绕点顺时针旋转，使菱形的对角线恰好与菱形的边在同一条直线上，原问题中的其他条件不变（如图13）．你在（1）中得到的两个结论是否发生变化？写出你的猜想并加以证明．

    3.若图（12）中，将菱形绕点顺时针旋转任意角度，原问题中的其他条件不变，请你直接写出的值（用含的式子表示）．

    解：（1）线段与的位置关系是          ；         ．

     

    查看答案和解析>>


    同步练习册答案