
题目列表(包括答案和解析)
观察是思考的“外壳”,要想思考得好,一定要善于观察.数学家在发现或解决问题时往往首先依赖于他对若干现象的观察--通过观察,如果发现某种值得注意的规律,就对它进行研究,并力图从中发现某种结论,去解释或描述这种模型,以求问题的顺利解决.例如,如果让你用任意方法去切一块圆饼,只要通过同一点不超过两刀,那么最多能得到几块?
自然,我们用不着特地去买一块饼来,只要在纸上画一些圆就行了.我们对各圆进行不同次数的切割,并在表中记录结果,得到:

我们仔细考查一下这张表,看看能否找到其中的规律.从记录上看,增加的块数分别是自然数1,2,3.切割次数也分别是1,2,3.这种规律是否继续有效呢?让我们再多试几次,并记录数据,得到:

现在的增加数分别是1,2,3,4,5,可见规律继续有效.这种规律使我们预测到:切割6次得22块,切割7次得29块.并进一步能使我们预测切割任意次所得的块数.
想一想:切割8次、9次将分别得到多少块?

| 分组 | 151.5-154.5 | 154.5-157.5 | 157.5-160.5 | 160.5-163.5 | 163.5-166.5 | 合计 |
| 频数 | 4 | 16 | 4 | |||
| 频率 | 0.10 | 0.25 | 0.4 | 0.10 | 100 |
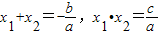 .我们把它们称为根与系数关系定理.
.我们把它们称为根与系数关系定理.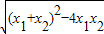 =
=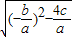 =
=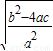 =
=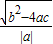
若x1,x2是关于x的一元二次方程ax2+bx+c=0(a≠0)的两个根,则方程的两个根x1,x2和系数a,b,c有如下关系:x1+x2=-![]() ,x1·x2=
,x1·x2=![]() .我们把它们称为根与系数关系定理.
.我们把它们称为根与系数关系定理.
如果设二次函数y=ax2+bx+c(a≠0)的图象与x轴的两个交点为A(x1,0),B(x2,0).利用根与系数关系定理我们又可以得到A、B两个交点间的距离为:
AB=|x1-x2|=![]() =
=![]() =
=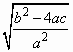 =
=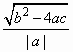 .
.
请你参考以上定理和结论,解答下列问题:
设二次函数y=ax2+bx+c(a>0)的图象与x轴的两个交点为A(x1,0),B(x2,0),抛物线的顶点为C,显然△ABC为等腰三角形.
(1)当△ABC为等腰直角三角形时,求b2-4ac的值;
(2)当△ABC为等边三角形时,求b2-4ac的值;
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com