
题目列表(包括答案和解析)
(如图所示)取一张矩形的纸进行折叠,具体操作过程如下:第一步:先把矩形ABCD对折,折痕为MN,如图(1);第二步:再把B点叠在折痕线MN上,折痕为AE,点B在MN上的对应点为![]() ,得Rt△
,得Rt△![]() ,如图(2);第三步:沿
,如图(2);第三步:沿![]() 线折叠得折痕EF,如图(3).利用展开图(4)探究:
线折叠得折痕EF,如图(3).利用展开图(4)探究:
(1)△AEF是什么三角形?证明你的结论;
(2)对于任一矩形,按照上述方法是否都能折出这种三角形?请说明理由.

(1)某广告公司设计员李叔叔设计的一份矩形样图如图(1)所示,他在矩形ABCD对角线AC上任意取一点P,过点P作EF∥BC,过点P作GH∥DC,EF和GH把矩形ABCD分为四个小矩形.他这样设计的目的是:使左上角矩形和右下角矩形相似,给人一种和谐的感觉.他的设计方法能使左上角矩形和右下角矩形相似吗?如果能,请说明理由.
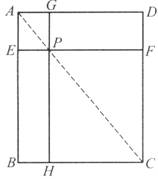
(1)
(2)如图(2),在设计过程中,李叔叔又尝试着过对角线上一点P画了两条斜线分别与矩形ABCD两组对边相交于点E,F,G,H,此时四边形AEPG与四边形CFPH还相似吗?为什么?
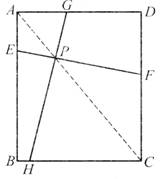
(2)
(3)赵叔叔认为,如图(3),只要四边形ABCD是平行四边形,那么过对角线AC上任意一点P作两条直线分别与两组对边相交于点E,F,G,H,上述结论都成立.你认为他说的对吗?
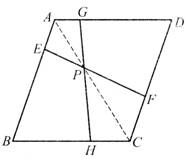
(3)

| 1 |
| 8 |
| x |
| y |

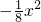 有几个公共点?
有几个公共点? 的值.
的值.
 有几个公共点?
有几个公共点? 的值.
的值.湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com