
题目列表(包括答案和解析)
如图,直线AB、CD相交于点O,因为∠1+∠3=180°.∠2+∠3=180°,所以∠1=∠2,它的推理依据是( ).
A
.同角的余角相等 B.等角的余角相等C.
同角的补角相等 D.等角的补角相等![]()
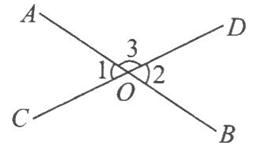
图3,直线AB与CD相交于点O,OP是∠BOC的平分线,OE⊥AB,OF⊥CD.
(1)写出图中(除直角相等外)两对相等的角:________与________、_______与________
(2)如果∠AOD=40°.
①那么根据 ,可得∠BOC= 度.
②因为OP是∠BOC的平分线,所以∠COP=![]() ∠ = 度.
∠ = 度.
③∠BOF=_____度.

如图,直线AB、CD交于点O,因为∠1+∠3=180°,∠2+∠3=180°,所以∠1=∠2,它的理论依据是
[ ]
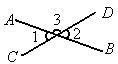
 如图,直线AB、CD交于点O,OE⊥AB,0为垂足,∠AOC=60°,求∠DOE的度数.(填空并添写理由)
如图,直线AB、CD交于点O,OE⊥AB,0为垂足,∠AOC=60°,求∠DOE的度数.(填空并添写理由)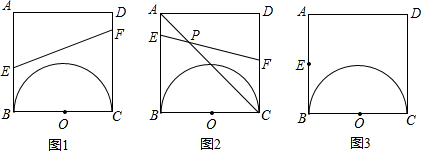
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com