
题目列表(包括答案和解析)
| 序号 | 方程 | 方程的解 | |||||
| 1 |
|
x1= | x2= | ||||
| 2 |
|
x1=4 | x2=6 | ||||
| 3 |
|
x1=5 | x2=8 | ||||
| … | … | … | … | ||||
| a |
| x |
| 1 |
| x-b |
| 年级 | ||||
| 身高(cm) | 七年级 | 八年级 | 九年级 | 总计(频数) |
| 143~153 | 12 | 3 | 0 | |
| 153~163 | 18 | 9 | 6 | |
| 163~173 | 24 | 33 | 39 | |
| 173~183 | 6 | 15 | 12 | |
| 183~193 | 0 | 0 | 3 |


| 图① | 图② | 图③ | |
| 三个角上三个数的积 | 1×(-1)×2=-2 | (-3)×(-4)×(-5)=-60 | |
| 三个角上三个数的和 | 1+(-1)+2=2 | (-3)+(-4)+(-5)=-12 | |
| 积与和的商 | -2÷2=-1, |


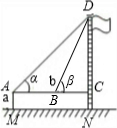
| 课题 | 测量校内旗杆高度 | ||
| 目的 | 运用所学数学知识及数学方法解决实际问题----测量旗杆高度 | ||
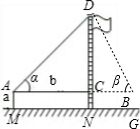
| 方案 | 方案一 | 方案二 | 方案三 |
示意图 |
 |
 |
|
| 测量工具 | 皮尺、测角仪 | 皮尺、测角仪 | |
| 测量数据 | AM=1.5m,AB=10m ∠α=30°,∠β=60° |
AM=1.5m,AB=20m ∠α=30°,∠β=60° |
|
| 计算过程(结 果保留根号) |
解: |
解: | |
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com