23．如下图.点D在AC上.∠DBC＝∠A..AC＝3.求CD的长.——青夏教育精英家教网—

23．如下图.点D在AC上.∠DBC＝∠A..AC＝3.求CD的长. 【查看更多】

题目列表(包括答案和解析)

如图，在四边形ABCD中，对角线AC与BD相交于点E，若AC平分∠DAB，且AB＝AE，AC＝AD，有如下四个结论：

①AC⊥BD；②BC＝DE；③∠DBC＝∠DAB；④△ABE是正三角形．

请写出正确结论的序号________(把你认为正确结论的序号都填上)．

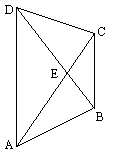
如图，在四边形ABCD中，对角线AC与BD相交于点E，若AC平分∠DAB，且AB＝AE，AC＝AD．有如下四个结论：

①AC⊥BD；②BC＝DE；

③∠DBC＝∠DAB；④△ABE是等边三角形．

请写出正确结论的序号________(把你认为正确结论的序号都写上)．

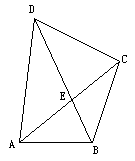
操作实验：

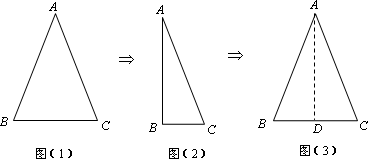
如图，把等腰三角形沿顶角平分线对折并展开，发现被折痕分成的两个三角形成轴对称．

所以△ABD≌△ACD，所以∠B＝∠C．

归纳结论：如果一个三角形有两条边相等，那么这两条边所对的角也相等．

根据上述内容，回答下列问题：

思考验证：

如图(4)，在△ABC中，AB＝AC．

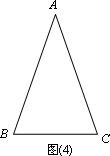
试说明∠B＝∠C的理由．(添加辅助线说明)

探究应用：

如图(5)，CB⊥AB，垂足为B，DA⊥AB，垂足为A．E为AB的中点，AB＝BC，CE⊥BD于F，连接DC、DE、AC，AC与DE交于点O．

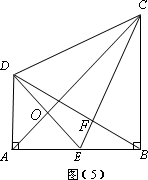
(1)BE与AD是否相等？为什么？

(2)小明认为AC垂直平分线段DE，你认为对吗？说说你的理由．

(3)∠DBC与∠DCB相等吗？试说明理由．

阅读下列材料：如图，⊙O1和⊙O2外切于点C，AB是⊙O1和⊙O2的外公切线，A、B为切点，求证：AC⊥BC．

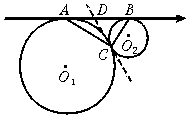
　　证实：过点C作⊙O1和⊙O2的内公切线交AB于D．

　　∵　DA、DC是⊙O1的切线，∴　DA＝DC．

　　∴　∠DAC＝∠DCA．同理∠DCB＝∠DBC．

　　又∵　∠DAC＋∠DCA＋∠DCB＋∠DBC＝180°，∴　∠DCA＋∠DCB＝90°．

　　即AC⊥BC．

　　根据上述材料，解答下列问题：

　　(1)在以上的证实过程中使用了哪些定理？请写出两个定理的名称或内容；

　　(2)以AB所在直线为x轴，过点C且垂直于AB的直线为y轴建立直角坐标系(如图11)．已知A、B两点的坐标为(-4，0)、(1，0)，求经过A、B、C三点的抛物线y＝ax2＋bx＋c的函数解析式；

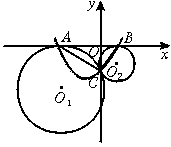
　　(3)根据(2)中所确定的抛物线，试判定这条抛物线的顶点是否落在两圆的连心O1O2上，并说明理由．

同步练习册答案