
题目列表(包括答案和解析)
(12分) 阅读并解答问题
用配方法可以解一元二次方程,还可以用它来解决很多问题.例如:因为 ,所以
,所以 就有最小值1,即
就有最小值1,即 ,只有当
,只有当 时,才能得到这个式子的最小值1.同样,因为
时,才能得到这个式子的最小值1.同样,因为 ,所以
,所以 有最大值1,即
有最大值1,即 ,只有在
,只有在 时,才能得到这个式子的最大值1.
时,才能得到这个式子的最大值1.

(1)当 = 时,代数式
= 时,代数式 有最 (填写大或小)值为 .
有最 (填写大或小)值为 .
(2)当 = 时,代数式
= 时,代数式 有最 (填写大或小)值为 .
有最 (填写大或小)值为 .
(3)矩形花园的一面靠墙,另外三面的栅栏所围成的总长度是16m,当花园与墙相邻的边长为多少时,花园的面积最大?最大面积是多少?
配方法可以用来解一元二次方程,还可以用它来解决很多问题。例如:因为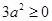 ,所以
,所以 ,即:
,即: 有最小值1,此时
有最小值1,此时 ;同样,因为
;同样,因为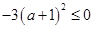 ,所以
,所以 ,即
,即 有最大值6,此时
有最大值6,此时  。
。
①当 =
时,代数式
=
时,代数式 有最 (填写大或小)值为
。②当
有最 (填写大或小)值为
。②当 =
时,代数式
=
时,代数式 有最 (填写大或小)值为
。
有最 (填写大或小)值为
。
③矩形花园的一面靠墙,另外三面的栅栏所围成的总长度是16m,当花园与墙相邻的边长为多少时,花园的面积最大?最大面积是多少?

 ,所以
,所以 就有最小值1,即
就有最小值1,即 ,只有当
,只有当 时,才能得到这个式子的最小值1.同样,因为
时,才能得到这个式子的最小值1.同样,因为 ,所以
,所以 有最大值1,即
有最大值1,即 ,只有在
,只有在 时,才能得到这个式子的最大值1.
时,才能得到这个式子的最大值1.
 = 时,代数式
= 时,代数式 有最 (填写大或小)值为 .
有最 (填写大或小)值为 . = 时,代数式
= 时,代数式 有最 (填写大或小)值为 .
有最 (填写大或小)值为 .(12分) 阅读并解答问题
用配方法可以解一元二次方程,还可以用它来解决很多问题.例如:因为![]() ,所以
,所以![]() 就有最小值1,即
就有最小值1,即![]() ,只有当
,只有当![]() 时,才能得到这个式子的最小值1.同样,因为
时,才能得到这个式子的最小值1.同样,因为![]() ,所以
,所以![]() 有最大值1,即
有最大值1,即![]() ,只有在
,只有在![]() 时,才能得到这个式子的最大值1.
时,才能得到这个式子的最大值1.

(1)当![]() = 时,代数式
= 时,代数式![]() 有最 (填写大或小)值为 .
有最 (填写大或小)值为 .
(2)当![]() = 时,代数式
= 时,代数式![]() 有最 (填写大或小)值为 .
有最 (填写大或小)值为 .
(3)矩形花园的一面靠墙,另外三面的栅栏所围成的总长度是16m,当花园与墙相邻的边长为多少时,花园的面积最大?最大面积是多少?
(12分) 阅读并解答问题
用配方法可以解一元二次方程,还可以用它来解决很多问题.例如:因为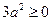 ,所以
,所以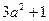 就有最小值1,即
就有最小值1,即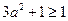 ,只有当
,只有当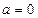 时,才能得到这个式子的最小值1.同样,因为
时,才能得到这个式子的最小值1.同样,因为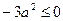 ,所以
,所以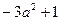 有最大值1,即
有最大值1,即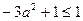 ,只有在
,只有在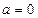 时,才能得到这个式子的最大值1.
时,才能得到这个式子的最大值1.
(1)当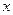 = 时,代数式
= 时,代数式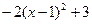 有最 (填写大或小)值为 .
有最 (填写大或小)值为 .
(2)当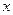 = 时,代数式
= 时,代数式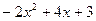 有最 (填写大或小)值为 .
有最 (填写大或小)值为 .
(3)矩形花园的一面靠墙,另外三面的栅栏所围成的总长度是16m,当花园与墙相邻的边长为多少时,花园的面积最大?最大面积是多少?
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com