
题目列表(包括答案和解析)
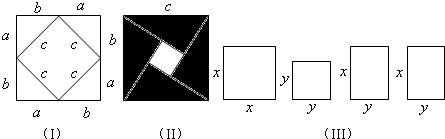
 如图为2002年国际数学家大会的会标,它可以看成由四个形状、大小完全相同的直角三角形拼成(其中较大的直角边长为a,较小的直角边长为b,斜边长为c),根据此图,回答下列问题:
如图为2002年国际数学家大会的会标,它可以看成由四个形状、大小完全相同的直角三角形拼成(其中较大的直角边长为a,较小的直角边长为b,斜边长为c),根据此图,回答下列问题: 如图为2002年国际数学家大会的会标,它可以看成由四个形状、大小完全相同的直角三角形拼成(其中较大的直角边长为a,较小的直角边长为b,斜边长为c),根据此图,回答下列问题:
如图为2002年国际数学家大会的会标,它可以看成由四个形状、大小完全相同的直角三角形拼成(其中较大的直角边长为a,较小的直角边长为b,斜边长为c),根据此图,回答下列问题:| 1 |
| 2 |
| 1 |
| 2 |
 ab),
ab), ab)由此推出勾股定理a2+b2=c2,这种根据图形可以极简单地直观推论或验证数学规律和公式的方法,简称“无字证明”.
ab)由此推出勾股定理a2+b2=c2,这种根据图形可以极简单地直观推论或验证数学规律和公式的方法,简称“无字证明”.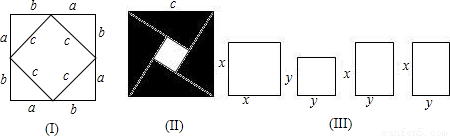
 ab),
ab), ab)由此推出勾股定理a2+b2=c2,这种根据图形可以极简单地直观推论或验证数学规律和公式的方法,简称“无字证明”.
ab)由此推出勾股定理a2+b2=c2,这种根据图形可以极简单地直观推论或验证数学规律和公式的方法,简称“无字证明”.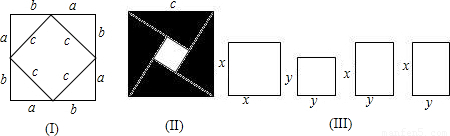
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com